In ΔABC,AC=BC and ∠BAC=70∘. Find ∠BCA
To solve the problem, we need to find the angle BCA in triangle ABC, where AC = BC and angle BAC = 70 degrees.
1. Identify the Given Information:
- Triangle ABC is isosceles because AC = BC.
- Angle BAC = 70 degrees.
2. Use the Properties of Isosceles Triangles:
- In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, if AC = BC, then angle ABC = angle ACB.
3. Let the Angles be Represented:
- Let angle ABC = angle ACB = x (since they are equal).
4. Apply the Triangle Sum Property:
- The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
Angle BAC+Angle ABC+Angle ACB=180∘
- Substituting the known values:
70∘+x+x=180∘
5. Simplify the Equation:
- Combine like terms:
70∘+2x=180∘
6. Isolate x:
- Subtract 70 degrees from both sides:
2x=180∘−70∘
2x=110∘
7. Solve for x:
- Divide both sides by 2:
x=110∘2=55∘
8. Find Angle BCA:
- Since angle BCA is equal to angle ABC, we have:
Angle BCA=x=55∘
Final Answer:
Angle BCA = 55 degrees.
---
- Triangle ABC is isosceles because AC = BC.
- Angle BAC = 70 degrees.
- In an isosceles triangle, the angles opposite the equal sides are equal. Therefore, if AC = BC, then angle ABC = angle ACB.
- Let angle ABC = angle ACB = x (since they are equal).
- The sum of the angles in any triangle is 180 degrees. Therefore, we can write the equation:
Angle BAC+Angle ABC+Angle ACB=180∘
- Substituting the known values:
70∘+x+x=180∘
- Combine like terms:
70∘+2x=180∘
- Subtract 70 degrees from both sides:
2x=180∘−70∘
2x=110∘
- Divide both sides by 2:
x=110∘2=55∘
- Since angle BCA is equal to angle ABC, we have:
Angle BCA=x=55∘
Angle BCA = 55 degrees.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question25videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 319videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
O is the circumcentre of ΔABC, given ∠BAC=85∘and∠BCA=55∘, find ∠OAC.
A40∘B50∘C60∘D80∘ - Question 2 - Select One
In △ABC, if AB=AC and ∠BAC=40∘ ,then the measure of ∠B is
त्रिभुज ABC में, यदि AB=AC है तथा ∠BAC=40∘ है, तो कोण B का मान क्या होगा ?A50∘B60∘C40∘D70∘ - Question 3 - Select One
In the given figure, side BC of ∠ABC is produced to D such that ∠ABC=70∘ and ∠ACD=120∘. Then, ∠ BAC = ?
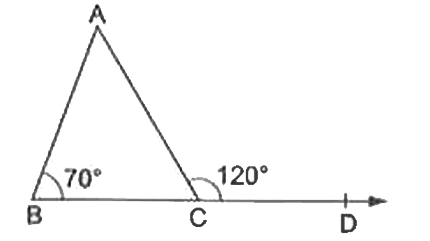 A60∘B50∘C70∘D35∘
A60∘B50∘C70∘D35∘
In ΔABC, ∠BAC=∠BCA=45∘, ∠ABC=90∘ then the value of AB.
 View Solution
View SolutionIn △ABC, right angled at B, if AB=6m and ∠BAC=30∘, find BC2+AC2
View SolutionIn a ΔABC,∠BCA=60∘andAB2=BC2+CA2+X. What is the value of X?
View SolutionIn ΔABC,∠ABC=70∘,∠BCA=40∘. O is the point of intersection of the perpendicular bisectors of the sides, then the angle ∠BOC is
View SolutionIn ΔABC,∠ABC=70∘,∠BCA=40∘. O is the point of intersection of the perpendicular bisectors of the sides, then the angle ∠BOC is
View Solution

