Construct a triange ABC in which AD,BE and CF are the medians with $A D = 5.4 c m, B E = 6$ cm and $C F = 8.1 c m$ .

Text Solution

Verified by Experts

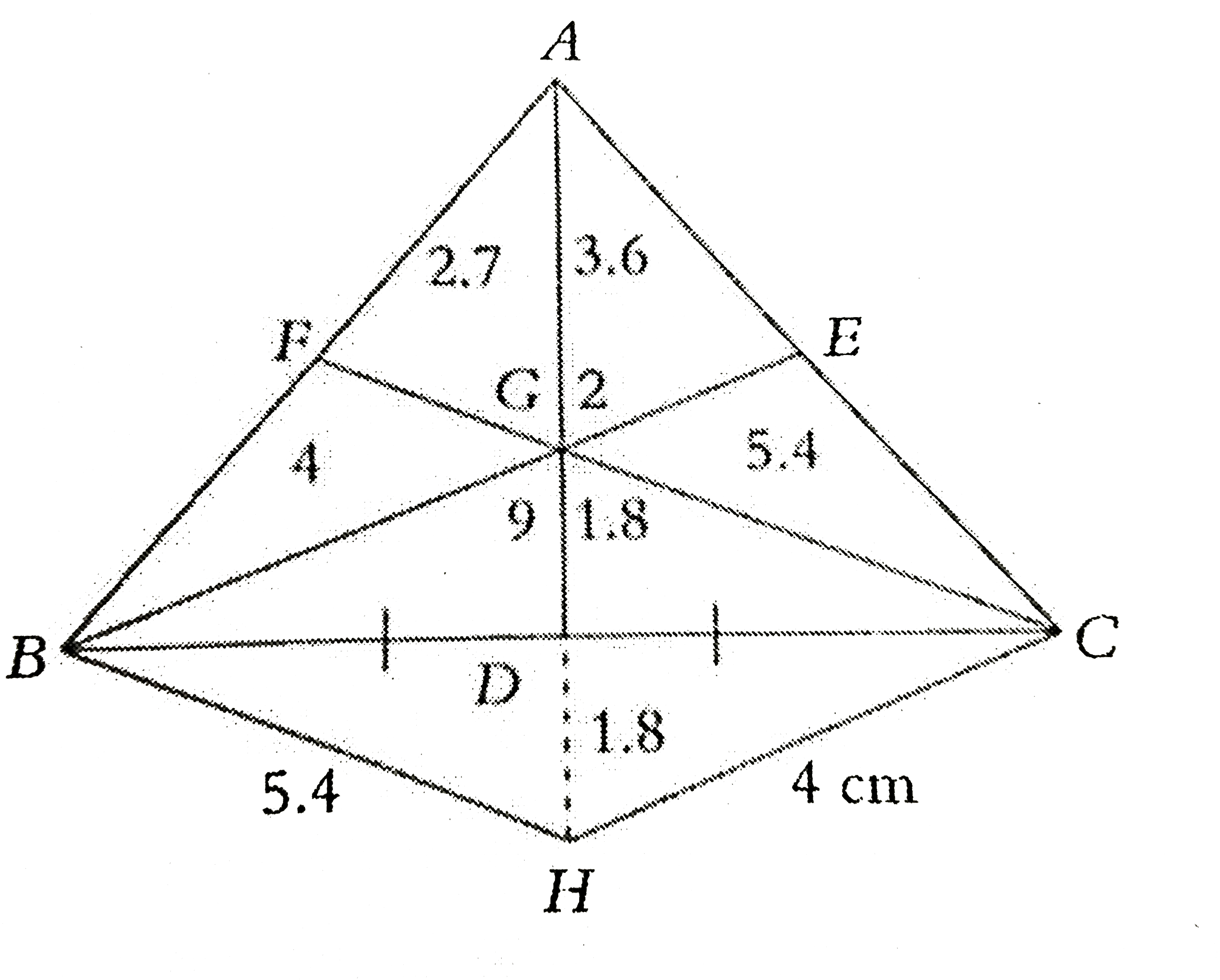
We know that the centroid G divides each median in the ratio $2 : 1$ from the corresponding vertex.
(a) $A G = 3.6 c m, G D = 1.8 c m$ ${∵ A D = 5.4 c m}$
(b) $B G = 4 c m, G E = 2 c m$ ${∵ B E = 6 c m}$
(c ) $C G = 5.4 c m, G F = 2.7 c m$ ${∵ C F = 8.1 c m}$
Produce $¯ ¯¯¯¯ ¯ G D$ to the point H such that $G D = D H = 1.8$ cm.
Now, BGCH is a parallelogram.

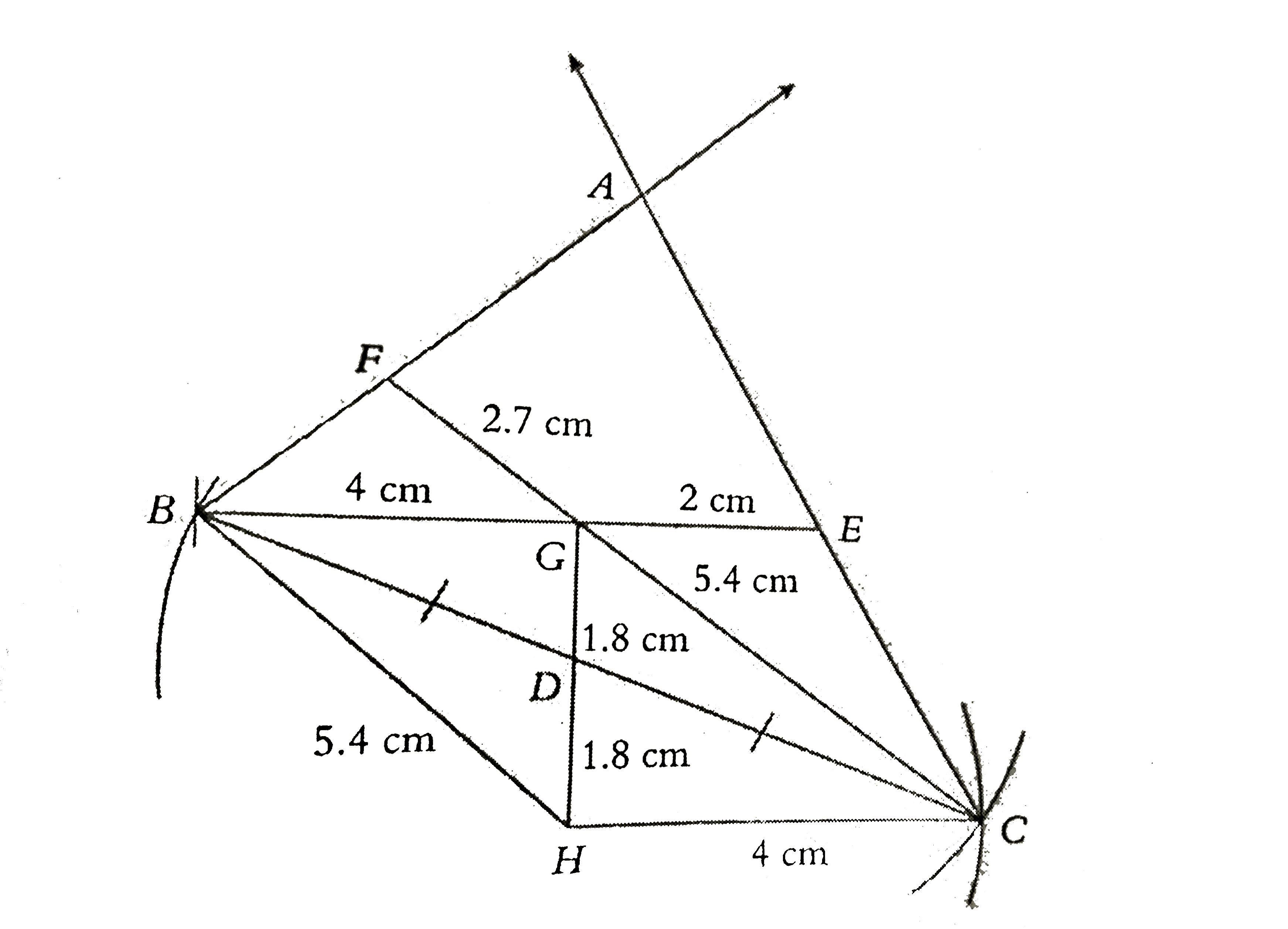
(a) Draw a parallelogram BGCH with $B H = C G = 5.4 c m, H C = B G = 4 c m$ and $G H = 3.6 c m$ .
(b) Join BC.
(c) Produce BG to the point E such that $G E = 2 c m$ .
(d ) Produce CG to the point such that $G F = 2.7$ cm.
(e) Join BF and CE and produce them to meet at point A.
ABC is the required triangle.

Updated on:21/07/2023

In a $Δ A B C, A D, B E$ and CF are three medians. The perimeter of $Δ A B C$ is always.
Aequal to $(¯ ¯¯¯¯ ¯ A B + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
Bgreater than $(¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
Cless than $(¯ ¯¯¯¯ ¯ A D + ¯ ¯¯¯¯ ¯ B E + ¯ ¯¯¯¯ ¯ C F)$
DNone of these
If in a triangle ABC, BE and CF are two medians perpendicular to each other and if $A B = 19$ cm and $A C = 22 c m$ then the length of BC is
A19.5 cm
B26 cm
C20.5 cm
D13 cm
In triangle ABC, AD, BE and CF are the medians intersecting at point G and area of triangle ABC is $156 c m^{2}$ . What is the area (in $c m^{2}$ ) of triangle FGE ?
A13
B26
C39
D52