Question

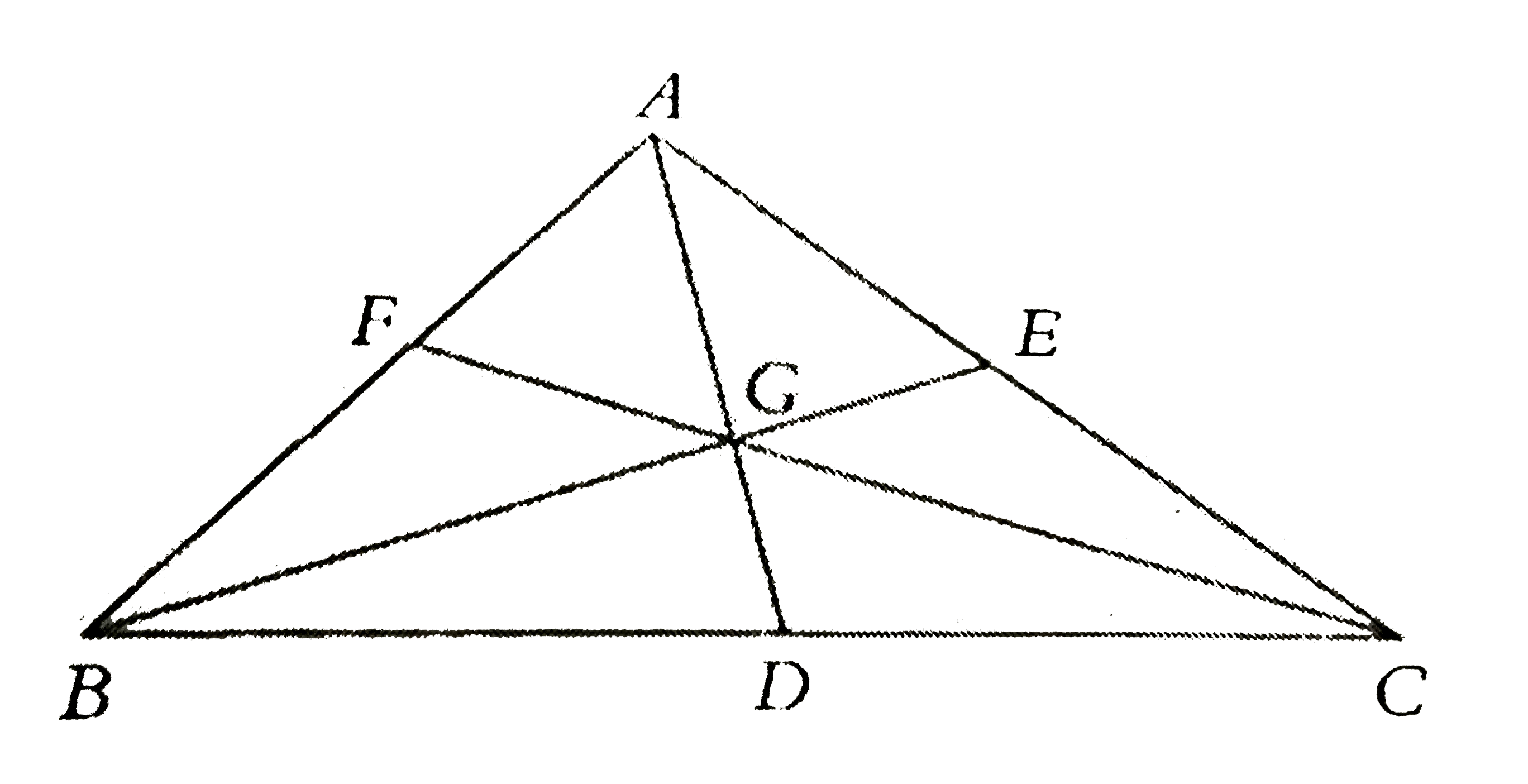
In A $\Delta ABC,AD,BE\text{and}CF$ are three medians . The perimeter of $\Delta ABC$ is always

Options

A. equal to ` ( bar(AD) + bar(BE) + bar(CF))`
B. Greater than `( bar(AD) + bar(BE) + bar(CF))`
C. less than ` ( bar(AD) + bar(BE) + bar(CF))`
D. None of these

Explanation

To solve the problem regarding the perimeter of triangle ABC in relation to its medians AD, BE, and CF, we can follow these steps:

Step 1: Understand the properties of medians
In triangle ABC, the medians AD, BE, and CF connect each vertex to the midpoint of the opposite side. The key property we will use is that the sum of any two sides of a triangle is greater than twice the length of the median that bisects the third side.

Step 2: Apply the property of medians
For triangle ABC, we can express the relationships as follows:
1. \( AB + AC > 2 \times AD \)
2. \( AB + BC > 2 \times BE \)
3. \( BC + AC > 2 \times CF \)

Step 3: Add the inequalities
Now, we will add all three inequalities together:
\( (AB + AC) + (AB + BC) + (BC + AC) > 2AD + 2BE + 2CF \)
This simplifies to:
\( 2AB + 2AC + 2BC > 2(AD + BE + CF) \)

Step 4: Simplify the equation
Dividing both sides by 2 gives us:
\( AB + AC + BC > AD + BE + CF \)
This means that the perimeter of triangle ABC (which is \( AB + AC + BC \)) is greater than the sum of the lengths of the medians (which is \( AD + BE + CF \)).

Step 5: Conclusion
Thus, we conclude that the perimeter of triangle ABC is always greater than the sum of its medians.

Final Result
\( \text{Perimeter of } \Delta ABC > AD + BE + CF \)