In the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.
Video Solution
Text Solution
AB=CD given
⇒∠AOB=∠COD=120∘
=∠OCD=∠ODC=180∘−∠COD2 (∵CO=OD)
∴∠OCD=180∘−120∘2=30∘

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very short answer type question25videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short Answer Type Questions 319videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 37videos
Formulae
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)7videos
INDICES
Similar Questions
Knowledge Check
- Question 1 - Select One
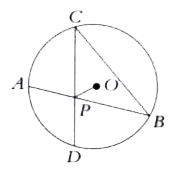
In the above figure , AB and CD are equal chords and O is the centre of the circle . If ∠OPB=50∘, then ∠PBC= ______ .A30∘B40∘C50∘D60∘ - Question 2 - Select One
In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘ - Question 3 - Select One
In the given figure, AB and CD are two common to the two touching circle. If CD=6cm, then AB is equal to
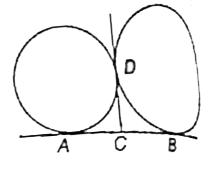 A9 cmB15 cmC12 cmDnone of the above
A9 cmB15 cmC12 cmDnone of the above
In the given figure,AB and BC are two chords of the circle with Centre O ,where ∠BAO=50∘,∠BCO=35∘,then ∠AOC is equal to
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View SolutionIn the given figure, O is the centre of a circle, ∠AOB=40∘ and ∠BDC=100∘, find ∠OBC.
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
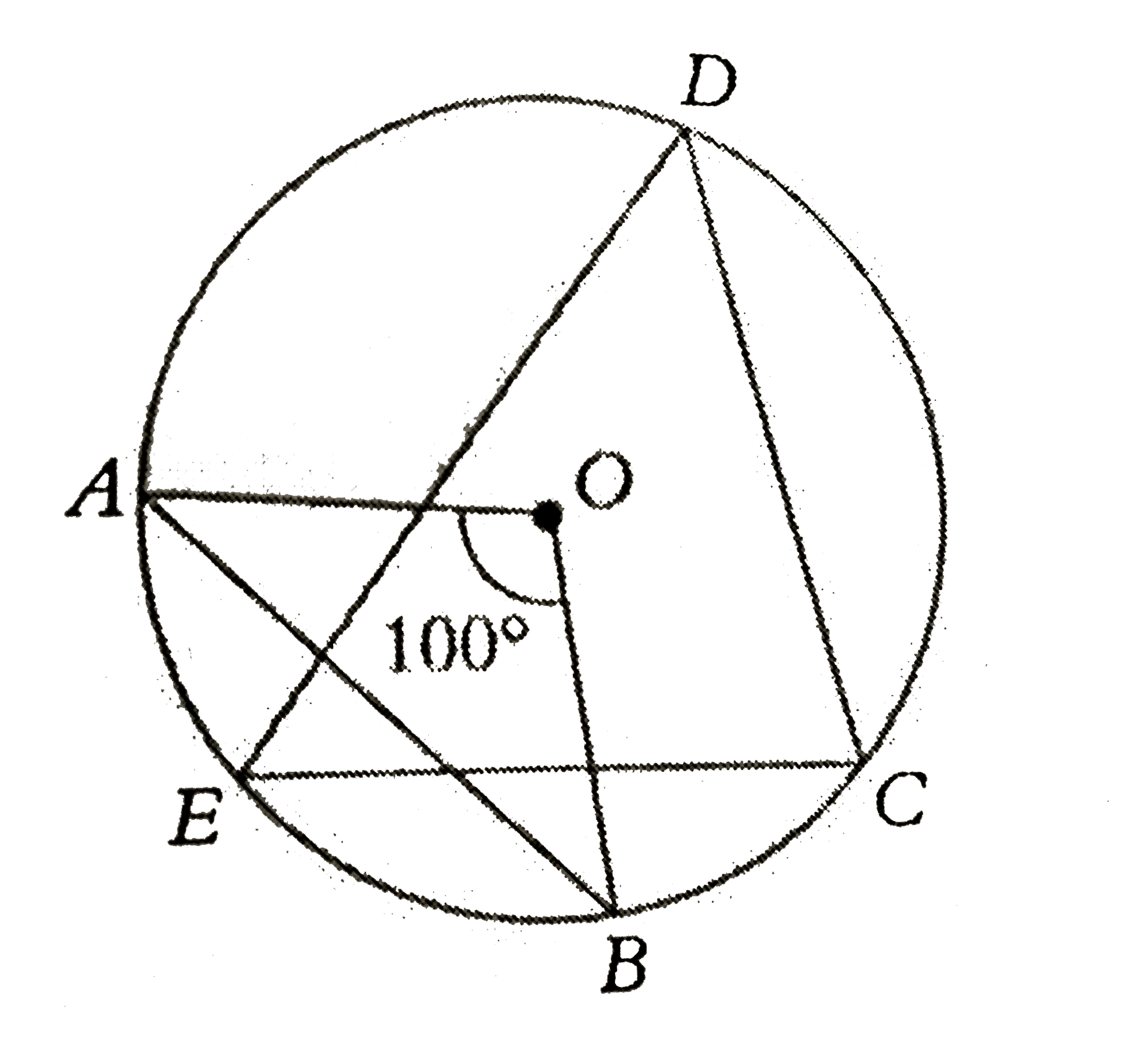 View Solution
View Solution

