In the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
Step by step video & image solution for In the given figure,AB" and "CDare equal chords of a circle with centre O .Prove that /_AOB~=/_COD and /_AOB=/_COD by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
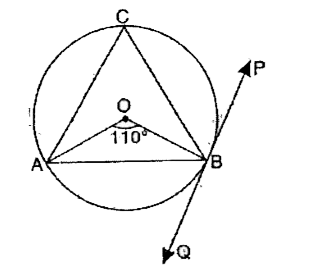 A45∘B70∘C55∘D35∘
A45∘B70∘C55∘D35∘In the given figure, BOD is the diameter of the circle with centre O. ∠COD=92∘and∠ABD=65∘. Then y equals
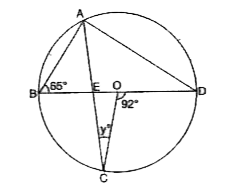 A65∘B46∘C44∘D21∘
A65∘B46∘C44∘D21∘
ABandCD are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that EB=ED.
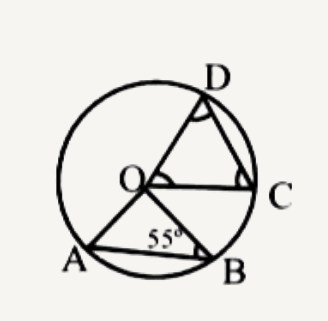
View SolutionIn the given figure, chords AB and CD are equal. If ∠OBA=55∘ then ∠COD is :
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘ and ∠APB=30∘, then 3(tan2∠APB+cot2∠COD) is equal to
View SolutionIn the given figure, AB∣∣CD and AB=CD, prove that:
 triangle AOB is congruent to triangle DOC.
triangle AOB is congruent to triangle DOC.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
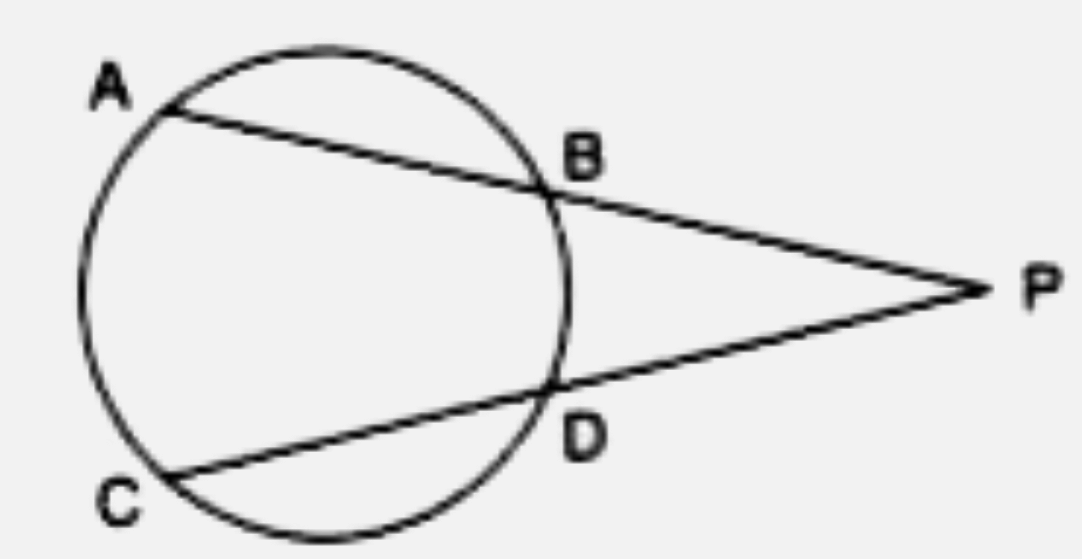
PB=PD
View Solution

