In the figure if P is (a,b,c) find the cordinates of A,B,C and D,E,F
The correct Answer is:a
To find the coordinates of points A, B, C, D, E, and F based on the given point P(a, b, c), we can analyze the positions of these points in relation to the axes in a 3D coordinate system.
1. Finding Coordinates of Point A:
- Point A lies on the x-axis.
- On the x-axis, the y-coordinate and z-coordinate are both 0.
- Therefore, the coordinates of point A are:
A=(a,0,0)
2. Finding Coordinates of Point B:
- Point B lies on the y-axis.
- On the y-axis, the x-coordinate and z-coordinate are both 0.
- Therefore, the coordinates of point B are:
B=(0,b,0)
3. Finding Coordinates of Point C:
- Point C lies on the z-axis.
- On the z-axis, the x-coordinate and y-coordinate are both 0.
- Therefore, the coordinates of point C are:
C=(0,0,c)
4. Finding Coordinates of Point D:
- Point D lies in the XY-plane.
- In the XY-plane, the z-coordinate is 0.
- The x-coordinate is the same as point P, which is a, and the y-coordinate is the same as point P, which is b.
- Therefore, the coordinates of point D are:
D=(a,b,0)
5. Finding Coordinates of Point E:
- Point E lies in the YZ-plane.
- In the YZ-plane, the x-coordinate is 0.
- The y-coordinate is the same as point P, which is b, and the z-coordinate is the same as point P, which is c.
- Therefore, the coordinates of point E are:
E=(0,b,c)
6. Finding Coordinates of Point F:
- Point F lies in the XZ-plane.
- In the XZ-plane, the y-coordinate is 0.
- The x-coordinate is the same as point P, which is a, and the z-coordinate is the same as point P, which is c.
- Therefore, the coordinates of point F are:
F=(a,0,c)
Summary of Coordinates:
- A=(a,0,0)
- B=(0,b,0)
- C=(0,0,c)
- D=(a,b,0)
- E=(0,b,c)
- F=(a,0,c)
- Point A lies on the x-axis.
- On the x-axis, the y-coordinate and z-coordinate are both 0.
- Therefore, the coordinates of point A are:
A=(a,0,0)
- Point B lies on the y-axis.
- On the y-axis, the x-coordinate and z-coordinate are both 0.
- Therefore, the coordinates of point B are:
B=(0,b,0)
- Point C lies on the z-axis.
- On the z-axis, the x-coordinate and y-coordinate are both 0.
- Therefore, the coordinates of point C are:
C=(0,0,c)
- Point D lies in the XY-plane.
- In the XY-plane, the z-coordinate is 0.
- The x-coordinate is the same as point P, which is a, and the y-coordinate is the same as point P, which is b.
- Therefore, the coordinates of point D are:
D=(a,b,0)
- Point E lies in the YZ-plane.
- In the YZ-plane, the x-coordinate is 0.
- The y-coordinate is the same as point P, which is b, and the z-coordinate is the same as point P, which is c.
- Therefore, the coordinates of point E are:
E=(0,b,c)
- Point F lies in the XZ-plane.
- In the XZ-plane, the y-coordinate is 0.
- The x-coordinate is the same as point P, which is a, and the z-coordinate is the same as point P, which is c.
- Therefore, the coordinates of point F are:
F=(a,0,c)
- A=(a,0,0)
- B=(0,b,0)
- C=(0,0,c)
- D=(a,b,0)
- E=(0,b,c)
- F=(a,0,c)
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12(A) (SHORT ANSWER TYPE QUESTIONS)8videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - MODERN PUBLICATIONCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12(B) (SHORT ANSWER TYPE QUESTIONS)5videos
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
- BOOK - MODERN PUBLICATIONCHAPTER - CONIC SECTIONS EXERCISE - CHAPTER TEST 1112videos
CONIC SECTIONS
- BOOK - MODERN PUBLICATIONCHAPTER - LIMITS AND DERIVATIVESEXERCISE - CHECK YOUR UNDERSTANDING10videos
LIMITS AND DERIVATIVES
Similar Questions
In the adoining figure if the coordinates of point P are (a,b,c) write the coordinates of A,B,C,D,E and F.
View SolutionIn figure ΔABC to an equalateral triangle with coordinate of BandC an B(1,0)andC(5,0) Find the co ordinate of value A.
View SolutionTriangles ABC and DEF are similar. If area (ABC)=36 cm2 , area (DEF)=64 cm2 and DE=6.2cm, find AB. (ii) If AB=1.2cm and DE=1.4cm , find the ratio of the areas of ABC and DEF .
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14ACView SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
 View Solution
View SolutionExamine the figures A, B, C, D, E and F. In which one of the four options all the items, A, B, C, D, E and Fare correct?
 View Solution
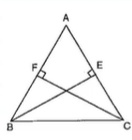
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
 View Solution
View SolutionFind the values of A,B,C,D,E,F,G in the following
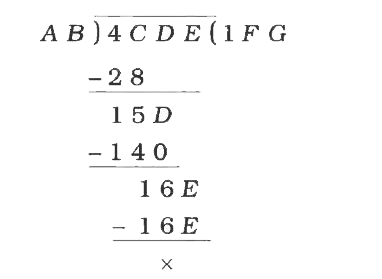 View Solution
View SolutionABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF) If the area of DFB=3 cm2, find the area of ^(gm) ABCD
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View Solution

