ABCD is a parallelogram in which BC is produced to E such that CE=BC.AE intersects CD at F. Prove that ar ( ADF)= ar ( ECF) If the area of DFB=3 cm2, find the area of ^(gm) ABCD
In △ADF and △ECF , we have
∠ADF=∠ECF [alt.int.∠s]
AD=EC [∵ AD=BCandBC=EC]
∠DFA=∠CFE [vert. opp. ∠s]
∴ By AAS congruence rule ,
△ADF≅△ECF
⇒ DF=CF [c.p.c.t.]
⇒ ar(△ADF)=ar(△ECF)
Now, DF=CF
⇒ BF is a median in △BDC
⇒ ar(△BDC)=2ar(△DFB)
=2×3=6cm2 [∵ar(△DFB) = 3 cm^2]
Thus, ar(∣∣gmABCD)=2ar(△BDC)
= 2×6=12cm2.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BFE)=ar(AFD)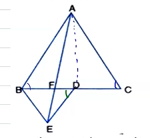
View SolutionIn Figure, ABC and BDE are two equilateral triangls such that D is the mid-point of BC.AE intersects BC in F. Prove that: ar ( BFE)= 2 ar (EFD)
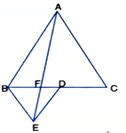
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F Prove that: ar(FED)=18ar(AFC)
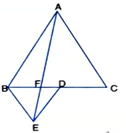
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=12ar(BAE)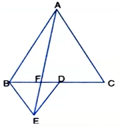
View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC

View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
View Solution