There are three evens $E_{1}, E_{2}$ and $E_{3}$ one of which must, and only one can happen. The odds are 7 to 4 against $E_{1}$ and 5 to 3 against $E_{2}$ . Find odds against $E_{3}$ .

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is: $65 : 23$

To solve the problem, we need to find the odds against event $E_{3}$ given the odds against events $E_{1}$ and $E_{2}$ .
1. Understand the Odds Against Events:
- The odds against $E_{1}$ are given as 7 to 4. This means for every 7 unfavorable outcomes, there are 4 favorable outcomes.
- The odds against $E_{2}$ are given as 5 to 3. This means for every 5 unfavorable outcomes, there are 3 favorable outcomes.
2. Convert Odds to Probabilities:
- For $E_{1}$ :
$Probability of E_{1} = \frac{Favorable outcomes}{Total outcomes} = \frac{4}{4 + 7} = \frac{4}{11}$
- For $E_{2}$ :
$Probability of E_{2} = \frac{3}{3 + 5} = \frac{3}{8}$
3. Use the Property of Exhaustive Events:
- Since $E_{1}, E_{2},$ and $E_{3}$ are mutually exclusive and exhaustive events, we know:
$P (E_{1}) + P (E_{2}) + P (E_{3}) = 1$
- Substituting the known probabilities:
$\frac{4}{11} + \frac{3}{8} + P (E_{3}) = 1$
4. Find a Common Denominator:
- The least common multiple of 11 and 8 is 88. We convert the fractions:
$\frac{4}{11} = \frac{4 \times 8}{11 \times 8} = \frac{32}{88}$
$\frac{3}{8} = \frac{3 \times 11}{8 \times 11} = \frac{33}{88}$
5. Substitute and Solve for $P (E_{3})$ :
- Now we can substitute these values into the equation:
$\frac{32}{88} + \frac{33}{88} + P (E_{3}) = 1$
$\frac{65}{88} + P (E_{3}) = 1$
$P (E_{3}) = 1 - \frac{65}{88} = \frac{88 - 65}{88} = \frac{23}{88}$
6. Calculate Odds Against $E_{3}$ :
- The probability of $E_{3}$ is $\frac{23}{88}$ . The probability against $E_{3}$ is:
$P (not E_{3}) = 1 - P (E_{3}) = 1 - \frac{23}{88} = \frac{65}{88}$
- The odds against $E_{3}$ are given by the ratio of unfavorable outcomes to favorable outcomes:
$Odds against E_{3} = \frac{P (not E_{3})}{P (E_{3})} = \frac{\frac{65}{88}}{\frac{23}{88}} = \frac{65}{23}$
Final Answer:
The odds against $E_{3}$ are $65$ to $23$ .

Updated on:18/9/2024

|

Class 11 MATHS PROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

There are three events A, B, C one of which must and only one can happen; The odds are 8 to 3 against A, 5 to 2 against B; find the odds against C.
A $43 : 34$
B $34 : 43$
C $43 : 77$
D $77 : 43$
Three batteries of emf $E_{1}, E_{2}$ and $E_{3}$ and internal resistance $r_{1}, r_{2}$ and $r_{3}$ are connected as shown. The current through the battery of emf $E_{3}$ is zero if.

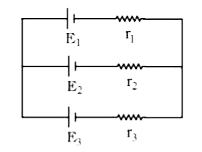A $E_{1} r_{2} + E_{2} r_{1} = E_{3} (r_{1} + r_{2})$
B $E_{1} r_{2} - E_{2} r_{1} = E_{3} (r_{1} + r_{2})$
C $E_{1} r_{2} + E_{2} r_{1} = E_{3} (r_{1} + r_{2})$
D $E_{1} r_{1} + E_{2} r_{2} = E_{3} (r_{1} + r_{2})$
In the circuit shown here, $E_{1} = E_{2} = E_{3} = 2 V$ and $R_{1} = R_{2} = 4 o h m s$ . The current flowing between point $A$ and $B$ through battery $E_{2}$ is

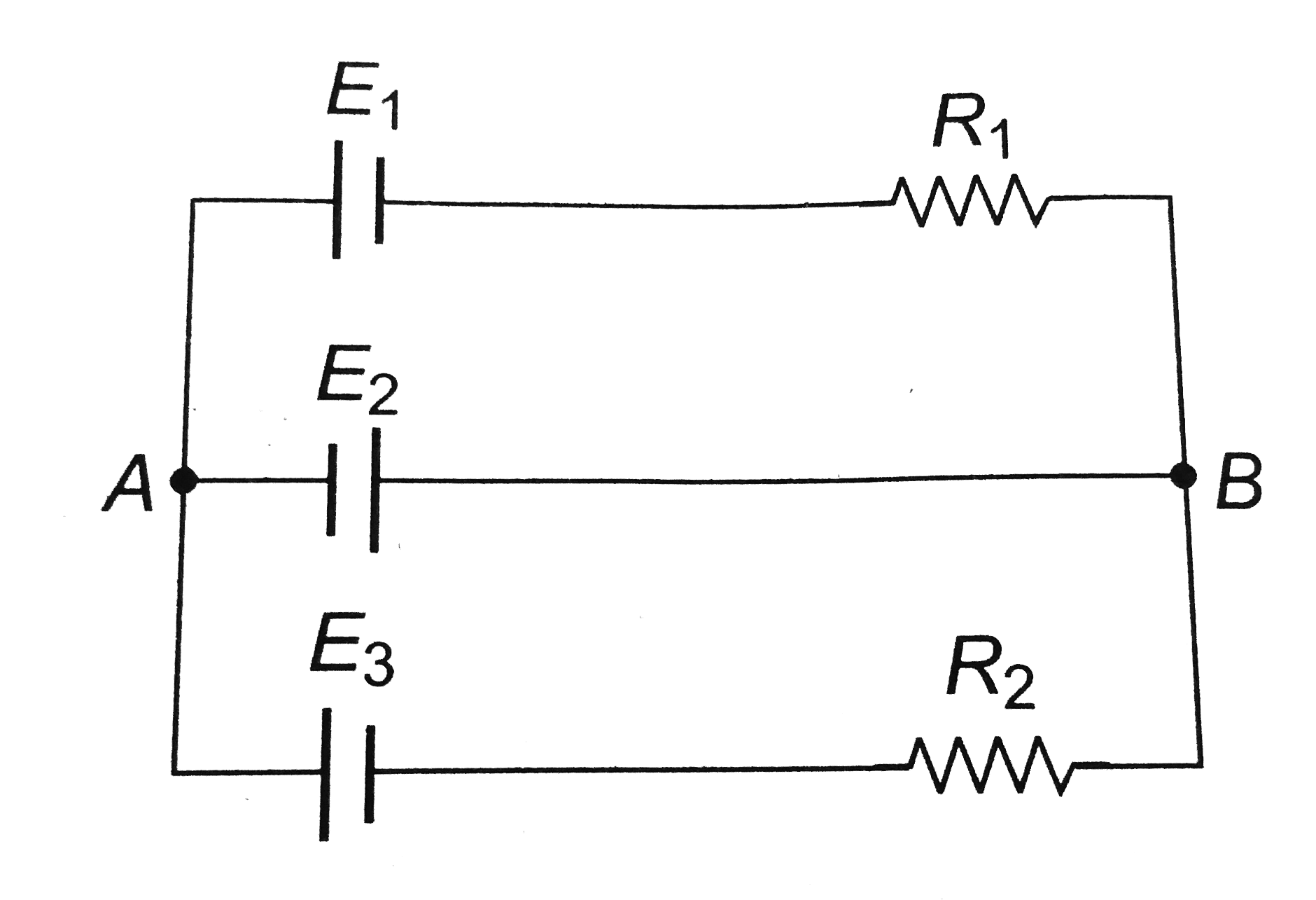AZero
B $2 a m p$ from $A$ to $B$
C $2 a m p$ from $B$ to $A$
DNone of the above

MODERN PUBLICATION-PROBABILITY-FAQs

Home
Ask Doubt
Profile