If performance of the students 'y' depends on the number of hours 'x' given by the relation :
y=4x−x22.
find the number of hours, the students work to have the best performance.
The correct Answer is:4 hours per day
To solve the problem of finding the number of hours x that students should work to achieve the best performance y, we will follow these steps:
Step 1: Write down the given function
The performance y is given by the equation:
y=4x−x22
Step 2: Differentiate the function
To find the maximum performance, we need to differentiate y with respect to x:
dydx=ddx(4x−x22)
Calculating the derivative:
dydx=4−12(2x)=4−x
Step 3: Set the derivative to zero
To find the critical points, we set the derivative equal to zero:
4−x=0
Solving for x:
x=4
Step 4: Verify if it is a maximum using the second derivative
Next, we need to check whether this critical point is a maximum by finding the second derivative:
d2ydx2=ddx(4−x)=−1
Since the second derivative is negative (−1<0), this indicates that the function y has a maximum at x=4.
Conclusion
Thus, the number of hours the students should work to achieve the best performance is:
4
The performance y is given by the equation:
y=4x−x22
To find the maximum performance, we need to differentiate y with respect to x:
dydx=ddx(4x−x22)
Calculating the derivative:
dydx=4−12(2x)=4−x
To find the critical points, we set the derivative equal to zero:
4−x=0
Solving for x:
x=4
Next, we need to check whether this critical point is a maximum by finding the second derivative:
d2ydx2=ddx(4−x)=−1
Since the second derivative is negative (−1<0), this indicates that the function y has a maximum at x=4.
Thus, the number of hours the students should work to achieve the best performance is:
4
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Type Questions (A. Multiple Choice Questions)45videos
APPLICATIONS OF DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Type Questions (B. Fill in the Blanks)10videos
APPLICATIONS OF DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - EXERCISE 1 (f) (Long Answer Type Questions (I))24videos
APPLICATIONS OF DERIVATIVES
- BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - CHAPTER TEST12videos
APPLICATIONS OF THE INTEGRALS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two positive numbers x and y satisfy the condition 4x2+25y2=20xy. Find the value of x : y.
A5:2B2:5C3:2D2:3 - Question 2 - Select One
The average of x numbers is y2 and the average of y numbers is x2 . Find the average of all the numbers taken together
Ax3+y3x+yBxyCx2+y2x+yDxy2+yx2 - Question 3 - Select One
The sum of the number of male and female students in an institute is 100. If the number of male students is x, then the number of female students becomes x % of the total number of students. Find the number of male students.
A(A) 60B(B) 65C(C) 50D(D) 45
The number of pairs (x,y) which will satisfy the equation x2−xy+y2=4(x+y−4) is
View SolutionThe given bar graph, shows the number of students in different classes.
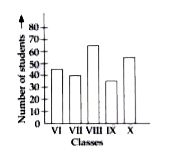
Find the total number of students in the classes VIII to X.View SolutionThe following table shows classification of number of workers and the number of hours they work in a software company. Find the median of the number of hours they work.
 View Solution
View SolutionThe following table shows classification of number of workers and the number of hours they work in a software company. Find the median of the number of hours they work.
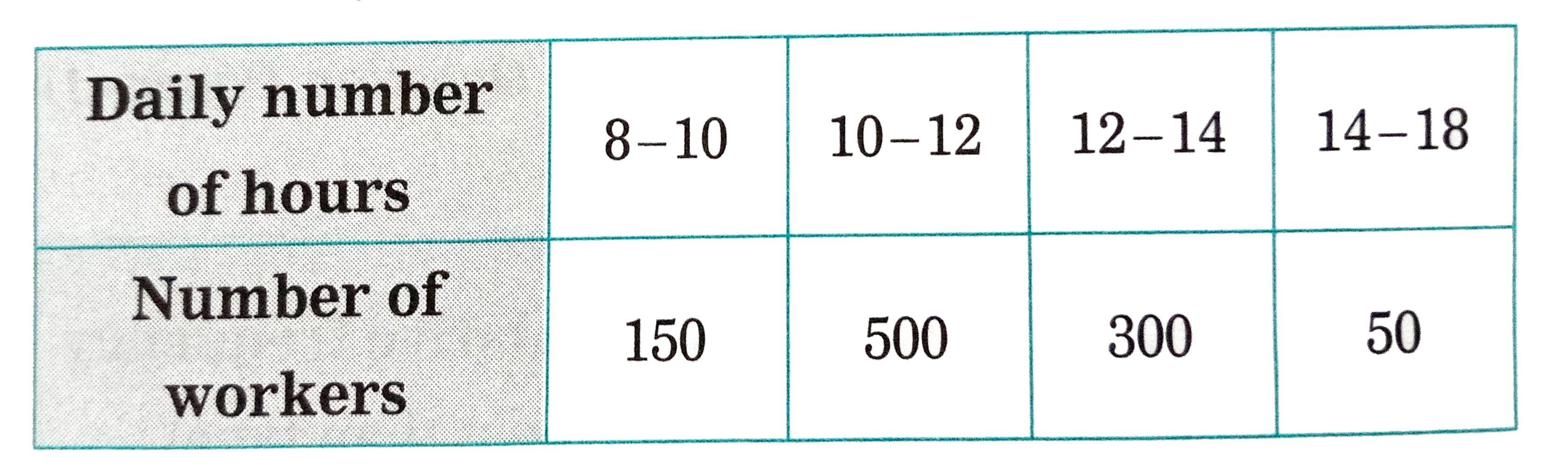 View Solution
View SolutionThe following table shows classification of number of workers and the number of hours they work in a software company.Find the median of the number of hours they work.
 View Solution
View Solution

