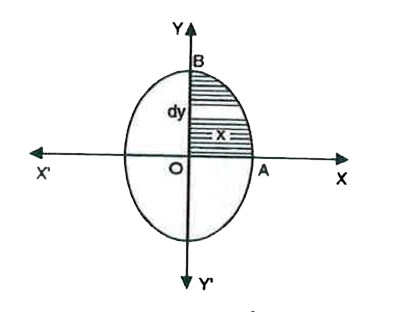
Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $4 (\frac{3 π}{2}) = 6 π$ sq. units

Answer

Step by step video, text & image solution for Find the area of the region bounded by the ellipse (x ^(2))/(4) + (y ^(2))/(9) =1. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - QUESTIONS FROM NCERT BOOK (EXERCISE 8.2)
7videos
APPLICATIONS OF THE INTEGRALS
BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - MISCELLANEOUS EXERCISE ON CHAPTER
19videos
APPLICATIONS OF THE INTEGRALS
BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS - SHORT ANSWER TYPE QUESTIONS
15videos
APPLICATIONS OF THE INTEGRALS
BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - CHAPTER TEST (1)
12videos
APPLICATIONS OF DERIVATIVES
BOOK - MODERN PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - CHAPTER TEST
12videos
CONTINUITY AND DIFFERENTIABILITY

Knowledge Check

Question 1 - Select One
Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.
A $\frac{3 π}{4}$ sq unit
B $\frac{3 π}{2}$ sq unit
C $\frac{9 π}{4}$ sq unit
D $\frac{4 π}{7}$ sq unit
Question 2 - Select One
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$
Question 3 - Select One
The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is
A $20 π sq units$
B $20 π^{2} sq units$
C $16 π^{2} sq units$
D $25 π sq units$

MODERN PUBLICATION-APPLICATIONS OF THE INTEGRALS -QUESTIONS FROM NCERT BOOK (EXERCISE 8.1)

Home
Ask Doubt
Profile

Find the area of the region bounded by the ellipse x24+y29=1.

The correct Answer is:4(3π2)=6π sq. units

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the area of the region bounded by the ellipse x29+y24=1 in fourth quadrant.

The area of the region bounded by the ellipse x225+y216=1 is

The area of the region bounded by the ellipse x225+y216=1 is

MODERN PUBLICATION-APPLICATIONS OF THE INTEGRALS -QUESTIONS FROM NCERT BOOK (EXERCISE 8.1)

Find the area of the region bounded by the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{9} = 1 .$

The correct Answer is: $4 (\frac{3 π}{2}) = 6 π$ sq. units

Find the area of the region bounded by the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ in fourth quadrant.

The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is

The area of the region bounded by the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ is