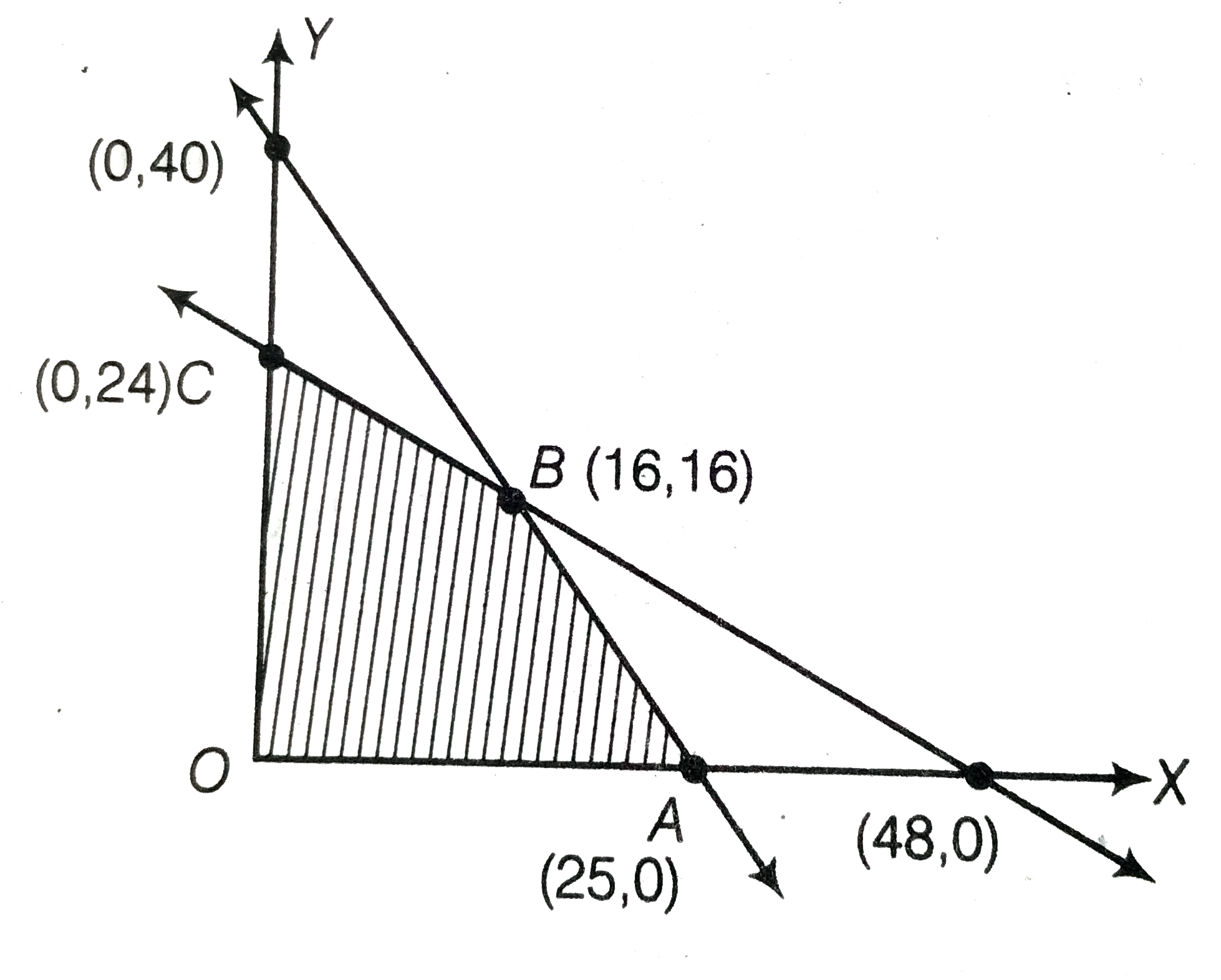
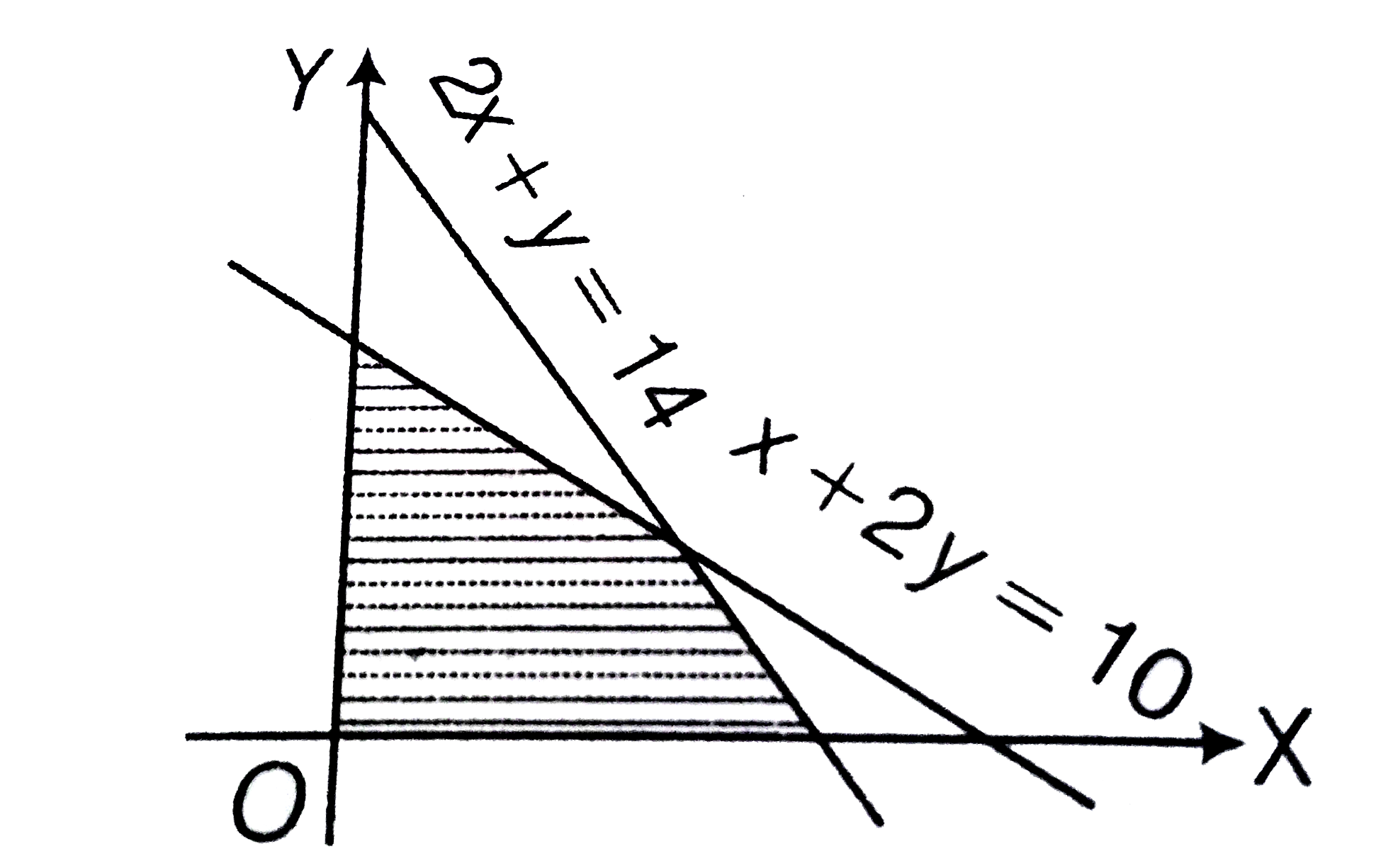
Determine the minimum value of Z=3x+2y (if any), if the feasible region for an LPP is shown in figure:
Minimum value of Z = 11.
Minimum value of Z = 14.
Minimum value of Z = 12.
Minimum value of Z = 13.
The correct Answer is:D
Step by step video, text & image solution for Determine the minimum value of Z = 3x + 2y (if any), if the feasible region for an LPP is shown in figure: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - FAQs9videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - (FAQ)18videos
LINEAR PROGRAMMING
- BOOK - MODERN PUBLICATIONCHAPTER - INVERSE - TRIGONOMETRIC FUNCTIONSEXERCISE - CHAPTER TEST (2)11videos
INVERSE - TRIGONOMETRIC FUNCTIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MATRICESEXERCISE - CHAPTER TEST (3)12videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
The corner point method for bounded feasible region comprises of the following steps
I. When the feasible region is bounded, M and m are the maximum and minimum values of Z.
II. Find the feasible region of the linear programming problem and determine its corner points.
Ill. Evaluate the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values of these points.
The correct order of these above steps isAIII,I,IIBII,III,ICII,I,IIIDI,III,II - Question 2 - Select One
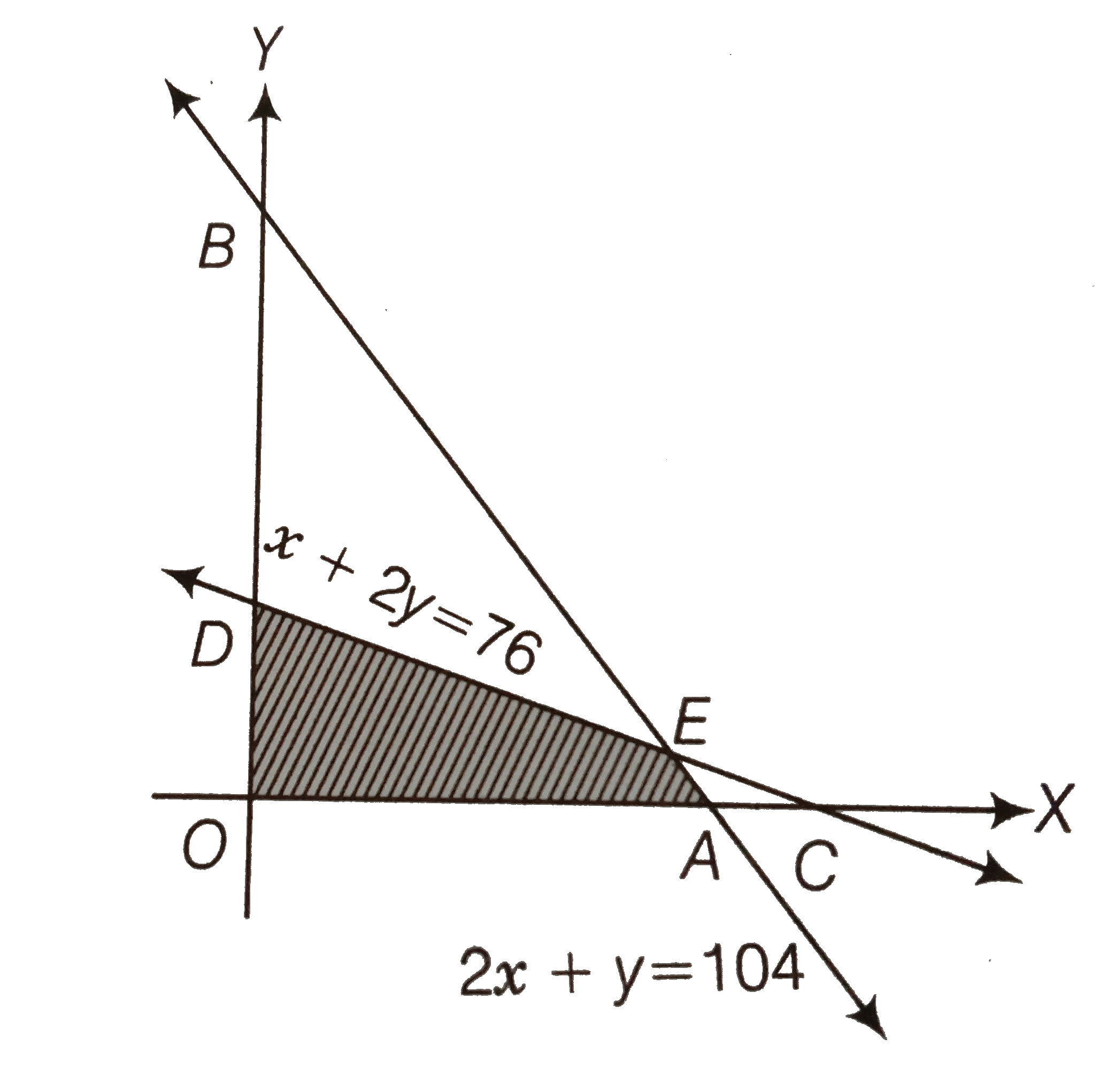
The feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.
 A22B23C24D21
A22B23C24D21 - Question 3 - Select One
Consider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?AI and IVBII and IIICI and IIIDII and IV
Find the maximum value of f(x,y)=3x+8y in following feasible region:
View SolutionThe maximum value of objective function Z=3x+y under given feasible region is
 View Solution
View SolutionThe maximum value of objective function z=2x+3y in the given feasible region is
 View Solution
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.
 View Solution
View SolutionIn a LPP, if the objective function Z=ax+by has the same maximum value of two corner points of the feasible region, then every point of the line segment joining these two points give the same ..value.
View Solution