Four point masses of 10 kg each are placed at the corners of a square PQRS of side 3 cm. Calculate the moment of inertia of the square about an axis coinciding with the side PQ of the square.
The correct Answer is:18×10−3kgm2
To calculate the moment of inertia of the square about an axis coinciding with the side PQ, we will follow these steps:
Step 1: Understand the Configuration
We have a square PQRS with each side measuring 3 cm. At each corner of the square, there is a point mass of 10 kg. The square is oriented such that the axis of rotation is along the side PQ.
Step 2: Identify the Relevant Masses
The masses at points P and Q will not contribute to the moment of inertia about the axis PQ because their distance from the axis is zero. Therefore, we only need to consider the masses at points R and S.
Step 3: Calculate the Distance of R and S from the Axis
The distance of point R from the axis PQ is equal to the side length of the square, which is 3 cm (or 0.03 m). The same applies to point S.
Step 4: Use the Moment of Inertia Formula
The moment of inertia I for a point mass is given by the formula:
I=mr2
where m is the mass and r is the distance from the axis of rotation.
Step 5: Calculate the Moment of Inertia for Points R and S
For point R:
IR=m⋅r2=10kg⋅(0.03m)2=10⋅0.0009=0.009kg m2
For point S:
IS=m⋅r2=10kg⋅(0.03m)2=10⋅0.0009=0.009kg m2
Step 6: Sum the Contributions
The total moment of inertia I about the axis coinciding with side PQ is the sum of the moments of inertia of points R and S:
I=IR+IS=0.009kg m2+0.009kg m2=0.018kg m2
Final Answer
The moment of inertia of the square about the axis coinciding with side PQ is:
I=0.018kg m2
---
We have a square PQRS with each side measuring 3 cm. At each corner of the square, there is a point mass of 10 kg. The square is oriented such that the axis of rotation is along the side PQ.
The masses at points P and Q will not contribute to the moment of inertia about the axis PQ because their distance from the axis is zero. Therefore, we only need to consider the masses at points R and S.
The distance of point R from the axis PQ is equal to the side length of the square, which is 3 cm (or 0.03 m). The same applies to point S.
The moment of inertia I for a point mass is given by the formula:
I=mr2
where m is the mass and r is the distance from the axis of rotation.
For point R:
IR=m⋅r2=10kg⋅(0.03m)2=10⋅0.0009=0.009kg m2
IS=m⋅r2=10kg⋅(0.03m)2=10⋅0.0009=0.009kg m2
The total moment of inertia I about the axis coinciding with side PQ is the sum of the moments of inertia of points R and S:
I=IR+IS=0.009kg m2+0.009kg m2=0.018kg m2
The moment of inertia of the square about the axis coinciding with side PQ is:
I=0.018kg m2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions
24 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY
8 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Four point masses of 5 g each are placed at the four corners fo a square of side 10 cm. Find the moment of inertia of the system (i) about an axis coinciding with one of the sides and (ii) about an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square.
View SolutionFour point masses of 20 g each are placed at the corners of a square ABCD of side 5 cm, as shown in Fig. 8.48. find the moment of inertia of the system (i) about an axis coinciding with the side BC and (ii) about an axis through A and perpendicular to the plane of the square.

View Solution
Knowledge Check
Four point masses, each of value m, are placed at the corners of a square ABCD of side 1. The moment of inertia of this system about an axis through A and parallel to BD is
Aml2B2ml2C√3ml2D3ml2Four point masses, each of value m, are placed at the corners of a square ABCD of side l. The moment of inertia of this system about an axis passing through A and parallel to BD is
A√3ml2B3ml2Cml2D2ml2Four point masses each of value m, are placed at the corners of a square ABCD of side l, The moment of inertia of the system about an axis passing throught A and parallel to BD is
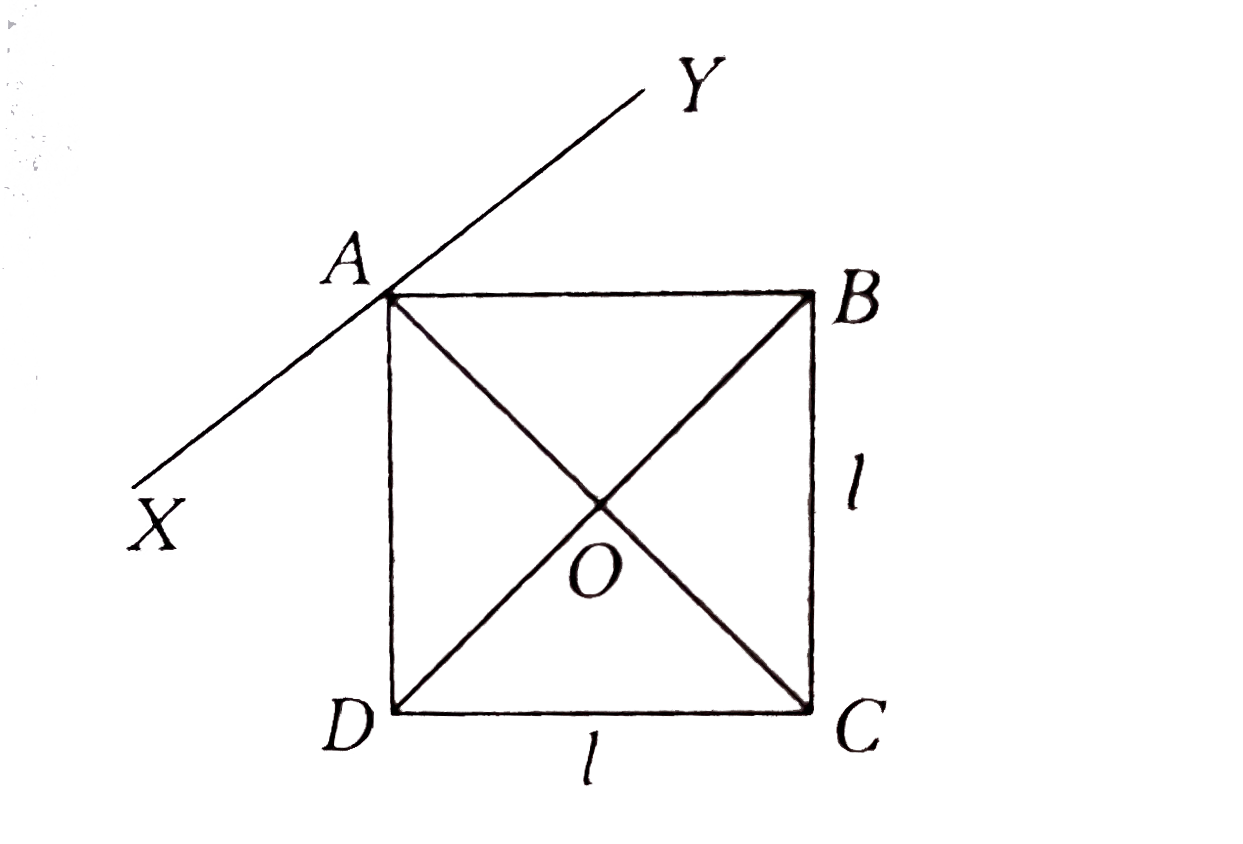 A√3ml2B3ml2Cml2D2ml2
A√3ml2B3ml2Cml2D2ml2
Four spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View SolutionFour spheres each of mass M and diameter 2a are placed at the corners of square of side b as shown below. Calculate the moment of inertia about axis AA'
View SolutionFour spheres each of mass M and diameter 2a are placed at the corners of square of side b as shown below. Calculate the moment of inertia about axis BB'
View Solution
