Show that →a.(→b×→c) is equal in magnitude to the volume of the parallelpiped formed by the vectors →a,→band→c
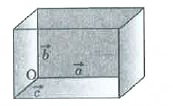
Let a parallelepiped is formed by three vectors →a,→band→c.
→b×→c=bcsin90∘ˆn=bcˆn
→a⋅(→v×→c)=→a⋅bcˆn=abccos0∘
=ab. (volume of parallelopiped)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT (ADDITIONAL EXERCISES) )
12 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS (OBJECTIVES QUESTIONS) (MULTIPLE CHOICE QUESTIONS (TYPE-I))
13 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY
8 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
The volume of the tetrahedron formed by the coterminous edges →a,→b,→c is 3. Then the volume of the parallelopiped formed by the coterminous edges →a+→b,→b+→c,→c+→a is
A36B34C32D30If the volume of the parallelepiped formed by the vectors →a×→b,→b×→cand→c×→a is 36 cubic units, then the volume (in cubic units) of the tetrahedron formed by the vectors →a+→b,→b+→cand→c+→a is equal to
A12B6C2D1If the volume of the parallelopiped formed by the vectors →a,→b,→c as three coterminous edges is 27 units, then the volume of the parallelopiped having →α=→a+2→b−→c,→β=→a−→b
and →γ=→a−→b−→c as three coterminous edges, isA27 cubic unitsB9 cubic unitsC81 cubic unitsDnone of these
Show that |→a|→b+∣∣→b∣∣→a is perpendicular to |→a|→b−∣∣→b∣∣→a for any two non zero vectors →aand→b.
View SolutionIf →a,→b,→c are mutually perpendicular vectors of equal magnitude show that →a+→b+→c is equally inclined to →a,→band→c
View SolutionStatement 1: If V is the volume of a parallelopiped having three coterminous edges as →a,→b, and →c, then the volume of the parallelopiped having three coterminous edges as
→α=(→a.→a)→a+(→a.→b)→b+(→a.→c)→c
→β=(→a.→b)→a+(→b.→b)→b+(→b.→c)→c
→γ=(→a.→c)→a+(→b.→c)→b+(→c.→c)→c is V3
Statement 2: For any three vectors →a,→b,→c
∣∣ ∣ ∣∣→a.→a→a.→b→a.→c→b.→a→b.→b→b.→c→c.→a→c.→b→c.→c∣∣ ∣ ∣∣=[→a→b→c]3
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .
.
View SolutionLet →a,→b,→c be three vectors of equal magnitude such that the angle between each pair is π3 . If ∣∣→a+→b+→c∣∣=√6 , " then " |→a|=
View Solution
