Question

Three point masses m1, m2, m3 are placed at the corners of an equilateral triangle of side 2 m. Locate the centre of mass of the system.
$m_1=2kg,m_2=3kg,m_3=4kg$

Explanation

To locate the center of mass of the system of three point masses $$m_1,m_2,m_3$$ placed at the corners of an equilateral triangle, we will follow these steps:

Step 1: Define the coordinates of the triangle's vertices
We have three masses located at the corners of an equilateral triangle with a side length of 2 m. We can place the triangle in the coordinate system as follows:
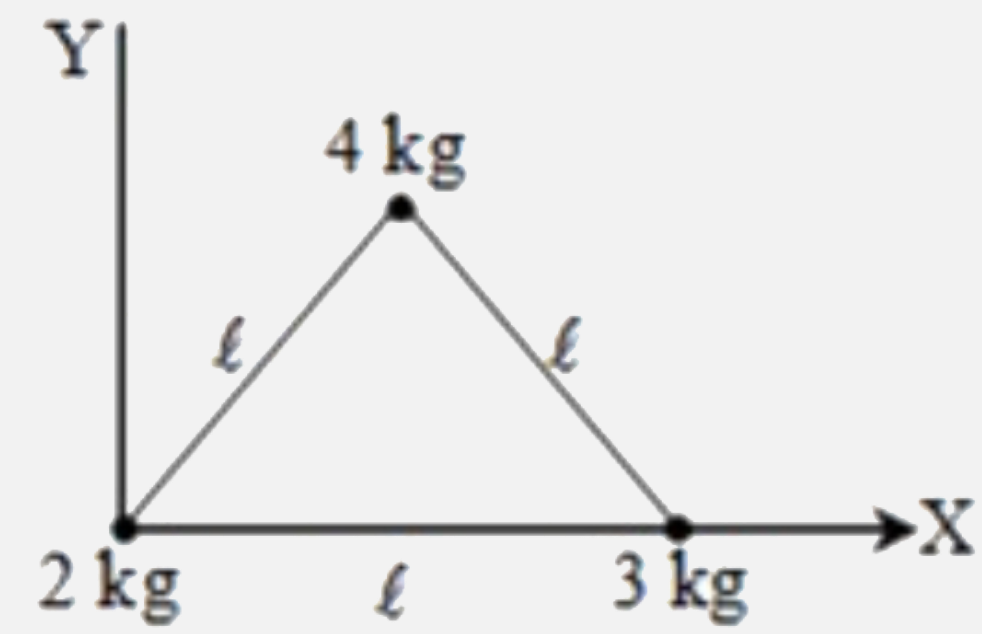
- Mass \( m_1 = 2 \, \text{kg} \) at \( A(0, 0) \)
- Mass \( m_2 = 3 \, \text{kg} \) at \( B(2, 0) \)
- Mass \( m_3 = 4 \, \text{kg} \) at \( C(1, \sqrt{3}) \) (using the height of the triangle, which is \( \sqrt{3} \) when the side is 2 m)

Step 2: Calculate the total mass
The total mass \( M \) of the system is given by:
\( M = m_1 + m_2 + m_3 = 2 + 3 + 4 = 9 \, \text{kg} \)

Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate of the center of mass \( x_{cm} \) is calculated using the formula:
\( x_{cm} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{M} \)
Substituting the values:
\( x_{cm} = \frac{(2 \cdot 0) + (3 \cdot 2) + (4 \cdot 1)}{9} = \frac{0 + 6 + 4}{9} = \frac{10}{9} \approx 1.11 \, \text{m} \)

Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate of the center of mass \( y_{cm} \) is calculated using the formula:
\( y_{cm} = \frac{m_1 y_1 + m_2 y_2 + m_3 y_3}{M} \)
Substituting the values:
\( y_{cm} = \frac{(2 \cdot 0) + (3 \cdot 0) + (4 \cdot \sqrt{3})}{9} = \frac{0 + 0 + 4\sqrt{3}}{9} = \frac{4\sqrt{3}}{9} \approx 0.77 \, \text{m} \)

Step 5: Final coordinates of the center of mass
Thus, the center of mass of the system is located at:
\( (x_{cm}, y_{cm}) \approx (1.11 \, \text{m}, 0.77 \, \text{m}) \)

Summary
The center of mass of the system of three point masses located at the corners of an equilateral triangle is approximately at the coordinates \( (1.11 \, \text{m}, 0.77 \, \text{m}) \).

---