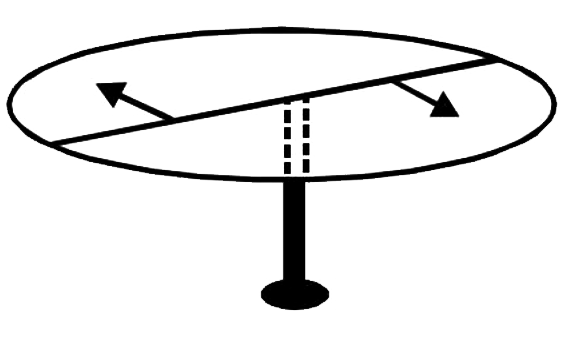
A horizontal circular platform of radius 0.5 m and mass axis. Two massless spring toy-guns, each carrying a steel ball of mass 0.05 kg are attached to the platform at a distance 0.25m from the centre on its either sides along its diameter (see figure). Each gun simultaneously fires the balls horizontally and perpendicular to the diameter in opposite directions. After leaving the platform, the balls have horizontal speed of 9ms−1 with respect to the ground. The rotational speed of the platform in rads−1 after the balls leace the platform is
The correct Answer is:4
Both the particles generate angular momentum about the centre in the same direction and disc rotates opposite to make total angunlr momentum zero.
2×0.5×9×0.25=(0.45×0.522)ω
2×0.05×9×0.25=0.45×0.252×ω
ω=4 rad/sec
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
1 Video
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionAn elevator platform is going up at a speed of 20m/s and during its upward motion a small ball of 50g mass, falling in downward direction, strikes the platform at speed 5m/s. Find the speed with which the ball rebounds.
View Solution
Knowledge Check
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
A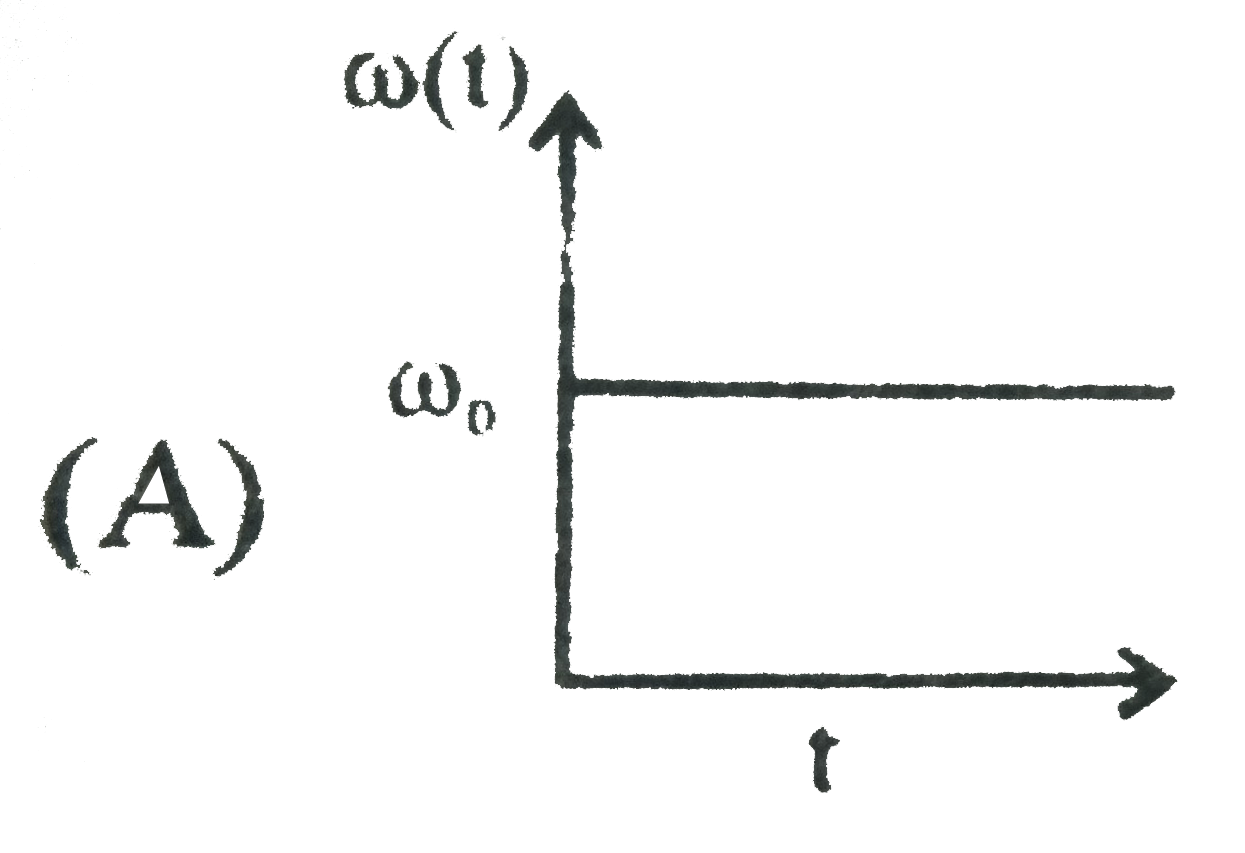 B
B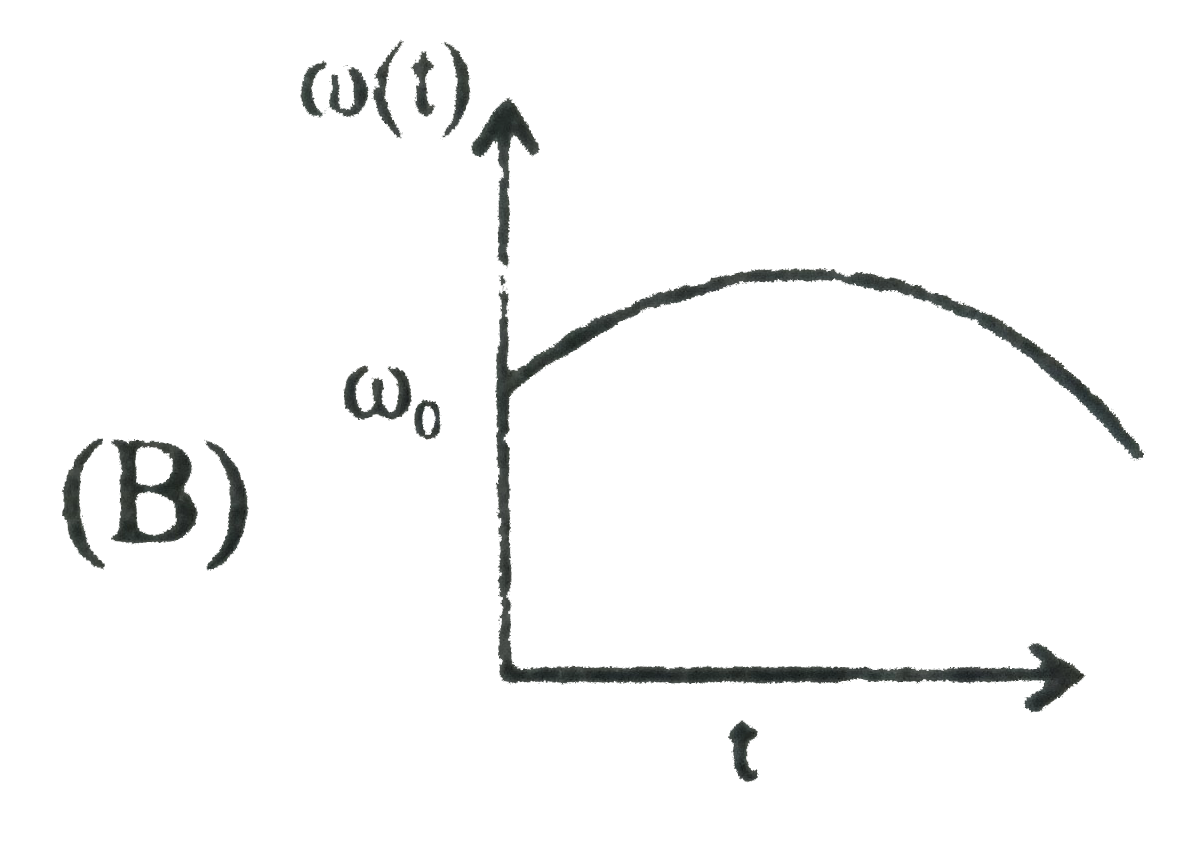 C
C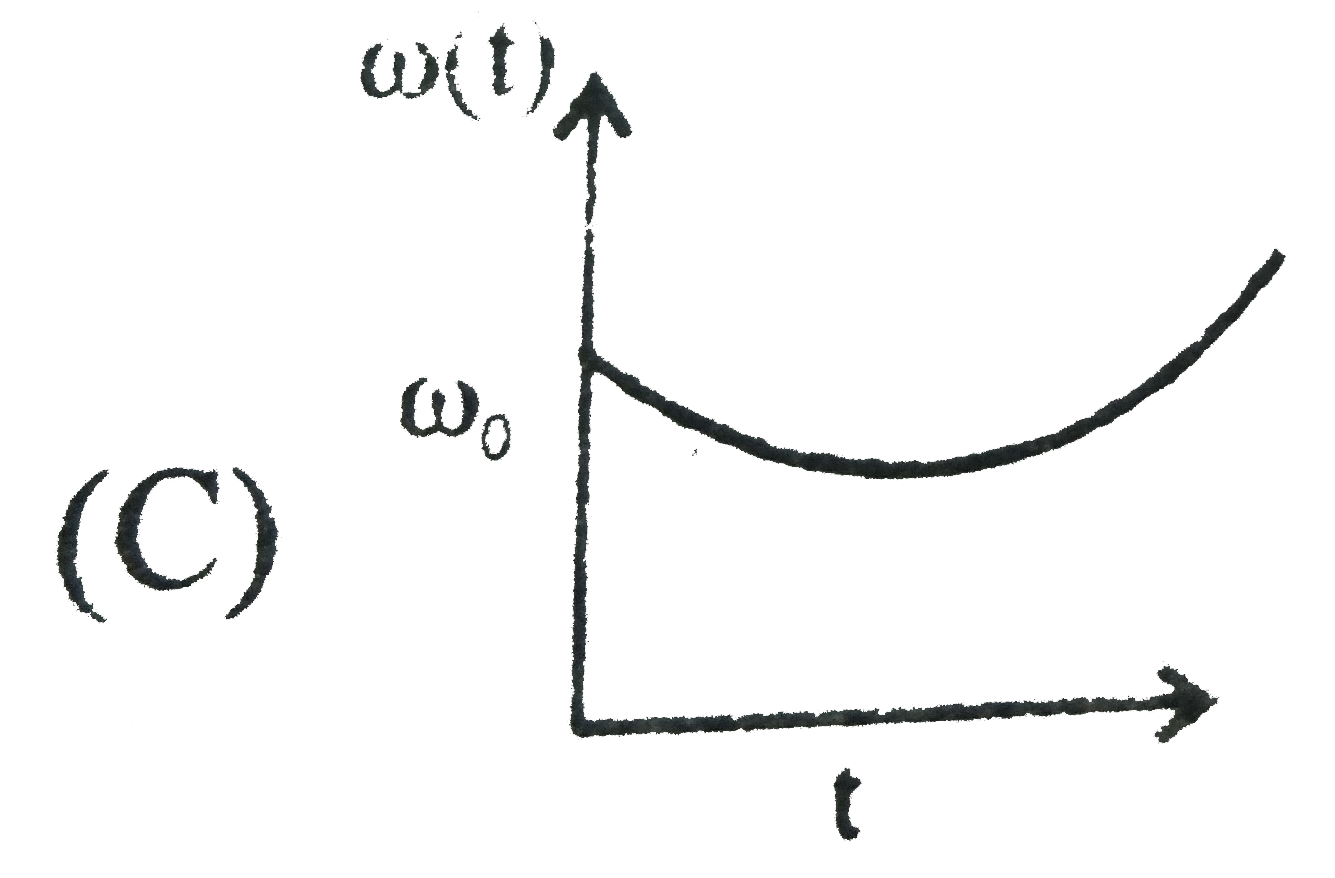 D
D
Three boys are standing on a horizontal platform of mass 170kg as shown in figure. The exchange their position as shown inthe figure. Distance moved by the platform is:
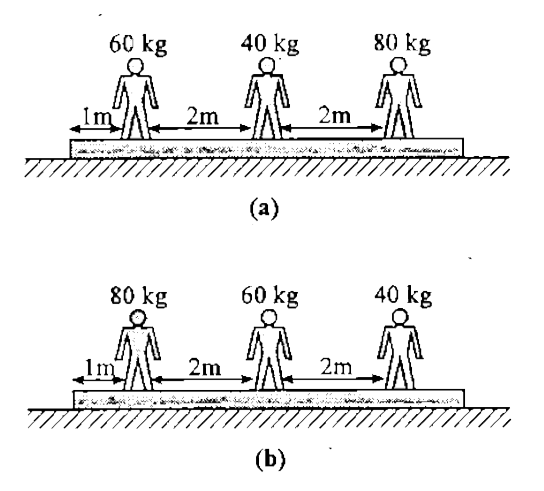 A0.35 mB0.55 mC0.45 mD0.25 m
A0.35 mB0.55 mC0.45 mD0.25 mA sphercial ball of mass 5kg is resting on a plane with angle of inclination 30∘ with respect to the horizontal as shown in the figure. The ball is held in place by a rope attached horizontally to the top of the ball and to the slope. The frictional force acting on the ball is
 A50NB2+√3NC502+√3D50√3N
A50NB2+√3NC502+√3D50√3N
A steel ball of mass 0.5 kg is dropped from a height of 4 m on to a horizontal heavy steel slab. The collision is elastic and the ball rebounds to its original height.
Calculate the impulse delivered to the ball during impact.
View SolutionA man of mass m1 = 80 kg is standing on a platform of mass m2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity vr = 10 m/s relative to the platform. Find the recoil speed of the platform.
View SolutionA man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. The man starts moving on the platform with a velocity vr relative to the platform. Find the recoil velocity of platform.
View SolutionA kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inerti of the platform is I . The system is at rest when a friend throws as ball of mas mand the kid cathces it. If the velocity of the ball is v horiontally along the tangent to the edge of the platform when it was caught by the kid find the angular speed of the platform after the event.
View SolutionA ball of mass m is projected from ground making an angle q to the horizontal. There is a horizontal wind blowing in the direction of motion of the ball. Due to wind the ball experiences a constant horizontal force of mg√3 in direction of its motion. Find θ for which the horizontal range of the ball will be maximum.
View Solution
