String is wrapped on a cylinder and free end of the string is pulled by a man as shown in figure. Horizontal surface is sufficiently rough. Person pulls l1 length of string and centre of the cylinder is found to move by a distance l2. Calculate l1/l2.
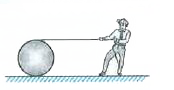
The correct Answer is:2
String is passing over the top point. When cylinder performs pure rolling then we know that speed of the top point is two times the speed of the centre of cylinder. Hence there will be same ratio for the distances involved
l1l2=2
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)16videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )1videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upward to prevent the centre of mass from falling as the string unwinds. Assume that the cylinder remains horizontal throughout and the thread does not slip. Find the length of the string unwound when the cylinder has reached an angular speed ω.
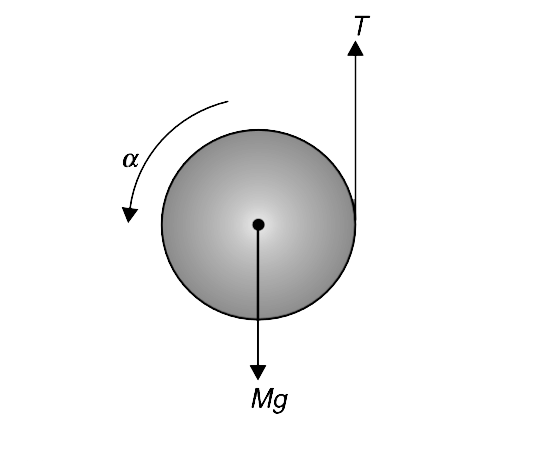 View Solution
View SolutionA string is wrapped around a cylinder of radius R and pulled at the top most point horizontally by a force F The cylinder rolls without slipping on the horizontal surface. The work done by the force by the time the cylinder makes one full rotation is
View Solution
Knowledge Check
- Question 1 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6 - Question 2 - Select One
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
AMg6BMg3CMg2D2Mg3 - Question 3 - Select One
A string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
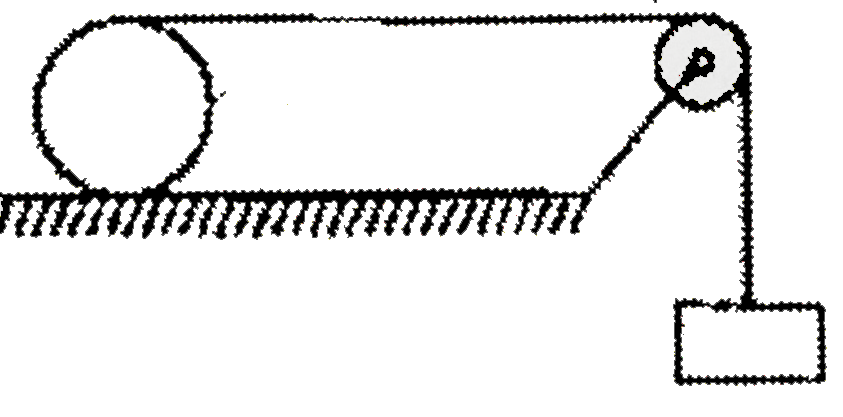
Acceleration of cylinder is:AgBg2Cg4D3g4
A cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravityView SolutionA string is wrapped around a cylinder of mass M and radius R(=2√2m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed ω(=5rad/s).(g=10ms2)
View SolutionFour blocks each of mass M connected by a massless strings are pulled by a force F on a smooth horizontal surface, as shown in figure.
 View Solution
View SolutionA string is wrapped several times round a solid cylinder. Then free end of the string is held stationary. If the cylinder is released to move down, then the acceleration of that cylinder is
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
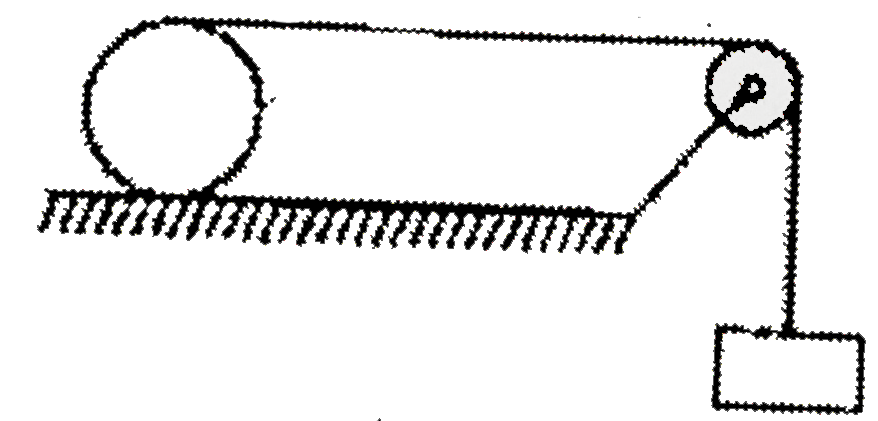
Velocity of point of contact 'of cylinder at this moment is:View Solution

