A cylinder of 4 m height is half filled with oil of density 0.72 g cm−3. If the Becond half of cylinder is filled with water, then find the pressure at the bottom of cylinder due to these liquids.
The correct Answer is:134712 Pascal
To find the pressure at the bottom of a cylinder that is half filled with oil and half filled with water, we will follow these steps:
Step 1: Understand the problem
We have a cylinder with a height of 4 m. The first half (2 m) is filled with oil of density 0.72 g/cm³, and the second half (2 m) is filled with water.
Step 2: Convert the density of oil to SI units
The density of oil is given as 0.72 g/cm³. We need to convert this to kg/m³:
0.72g/cm3=0.72×1000kg/m3=720kg/m3
Step 3: Identify the density of water
The density of water is known to be:
ρwater=1000kg/m3
Step 4: Calculate the pressure due to the oil
The pressure at the bottom of the cylinder due to the oil can be calculated using the formula:
Poil=ρoil⋅g⋅hoil
Where:
- ρoil=720kg/m3
- g=9.81m/s2 (acceleration due to gravity)
- hoil=2m
Substituting the values:
Poil=720kg/m3⋅9.81m/s2⋅2m=14107.2Pa
Step 5: Calculate the pressure due to the water
Similarly, the pressure due to the water can be calculated as:
Pwater=ρwater⋅g⋅hwater
Where:
- ρwater=1000kg/m3
- hwater=2m
Substituting the values:
Pwater=1000kg/m3⋅9.81m/s2⋅2m=19620Pa
Step 6: Calculate the total pressure at the bottom of the cylinder
The total pressure at the bottom of the cylinder is the sum of the pressures due to the oil and the water:
Ptotal=Poil+Pwater=14107.2Pa+19620Pa=33727.2Pa
Step 7: Convert the total pressure to Pascal
Since 1 Pa = 1 N/m², the total pressure at the bottom of the cylinder is:
Ptotal=33727.2Pa
Final Answer
The pressure at the bottom of the cylinder due to the oil and water is approximately:
Ptotal≈33727.2Pa or 3.37×104Pa
We have a cylinder with a height of 4 m. The first half (2 m) is filled with oil of density 0.72 g/cm³, and the second half (2 m) is filled with water.
The density of oil is given as 0.72 g/cm³. We need to convert this to kg/m³:
0.72g/cm3=0.72×1000kg/m3=720kg/m3
The density of water is known to be:
ρwater=1000kg/m3
The pressure at the bottom of the cylinder due to the oil can be calculated using the formula:
Poil=ρoil⋅g⋅hoil
Where:
- ρoil=720kg/m3
- g=9.81m/s2 (acceleration due to gravity)
- hoil=2m
Poil=720kg/m3⋅9.81m/s2⋅2m=14107.2Pa
Similarly, the pressure due to the water can be calculated as:
Pwater=ρwater⋅g⋅hwater
Where:
- ρwater=1000kg/m3
- hwater=2m
Pwater=1000kg/m3⋅9.81m/s2⋅2m=19620Pa
The total pressure at the bottom of the cylinder is the sum of the pressures due to the oil and the water:
Ptotal=Poil+Pwater=14107.2Pa+19620Pa=33727.2Pa
Since 1 Pa = 1 N/m², the total pressure at the bottom of the cylinder is:
Ptotal=33727.2Pa
The pressure at the bottom of the cylinder due to the oil and water is approximately:
Ptotal≈33727.2Pa or 3.37×104Pa
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Conceptual Questions29videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Problems9videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)12videos
MATHEMATICAL TOOLS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test15videos
MOTION IN A PLANE
Similar Questions
One third of a cylinder of 3 m height is filled with oil of density 0.62 g cm−3. and the rest of it is filled with mercury of density 13.6 g cm−3. Calculate the total pressure at the bottom of cylinder due to both oil and mercury.
View SolutionA vertical hollow cylinder of height 1.52m is fitted with a movable piston of negligible mass and thickness. The lower half of the cylinder contains an ideal gas and the upper half of the mercury comes out of the cylinder Find the temperature assuming the thermal expansion of mercury to be negligible .
View Solution
Knowledge Check
- Question 1 - Select One
A tank 5 m high is half filled with water and then is filled to the top with oil of density 0.85 g The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2 - Question 2 - Select One
A tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
A1.85g/cm2B89.25g/cm2C462.5g/cm2D500g/cm2 - Question 3 - Select One
A cylinder is filled with non viscous liquid of density d to a hegiht h0 and a hole is made at a height h1 from the bottom of the cylinder. The velocity of liquid issuing out of the hole is
A√(2gh0)B√2g(h0−h1)C√dgh1D√dgh0
A cylindrical vessel of radius 1 m and height 2 m is half filled with water. Find the centre of mass of the system consisting of cylinder and water. The cylinder has mass 10 kg per square metre of it and density of water 1000 kg m−3.
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is
 View Solution
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
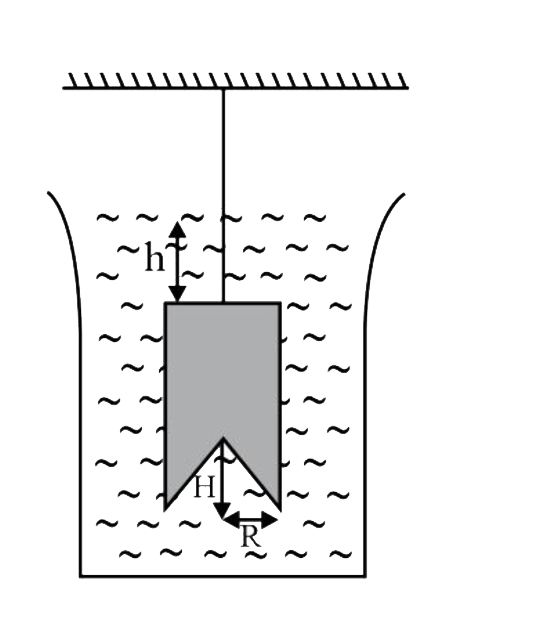 View Solution
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
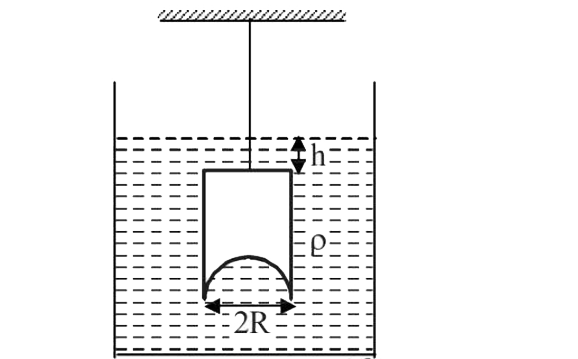 View Solution
View Solution

