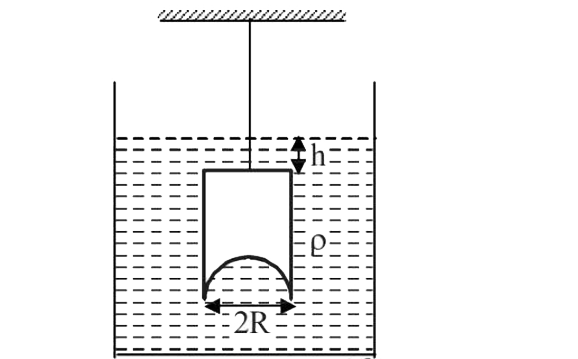
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
Mg
Mg-Vdg
Mg+πR2hdg
dg(V+πR2h)
The correct Answer is:D
The net upward force on the bottom of cylinder = Weight of liquid displaced by cylinder + thrust on the upper surface of cylinder to h column of liquid .
=Vdg+hdg×πR2
=dg(V+πR2h)
Topper's Solved these Questions
- THRUST AND PRESSUREBook:MTG IIT JEE FOUNDATIONChapter:THRUST AND PRESSUREExercise:Exercise (Match the following)
Explore 5 Videos
- THRUST AND PRESSUREBook:MTG IIT JEE FOUNDATIONChapter:THRUST AND PRESSUREExercise:Exercise (Assertion & Reason type)
Explore 10 Videos
- THRUST AND PRESSUREBook:MTG IIT JEE FOUNDATIONChapter:THRUST AND PRESSUREExercise:NCERT Section
Explore 10 Videos
- SOUNDBook:MTG IIT JEE FOUNDATIONChapter:SOUNDExercise:Olympiad/HOTS Corner
Explore 15 Videos
- WORK AND ENERGYBook:MTG IIT JEE FOUNDATIONChapter:WORK AND ENERGYExercise:Olympaid/HOTS Corner
Explore 20 Videos
Similar Questions
Knowledge Check
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is
 AMgBMg - h ρ gCMg+πR2hρgDρg(V+πR2h)
AMgBMg - h ρ gCMg+πR2hρgDρg(V+πR2h)A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
 AMgBMg-VdgCMg+πR2hdgDdg(V+πR2h)
AMgBMg-VdgCMg+πR2hdgDdg(V+πR2h)A conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
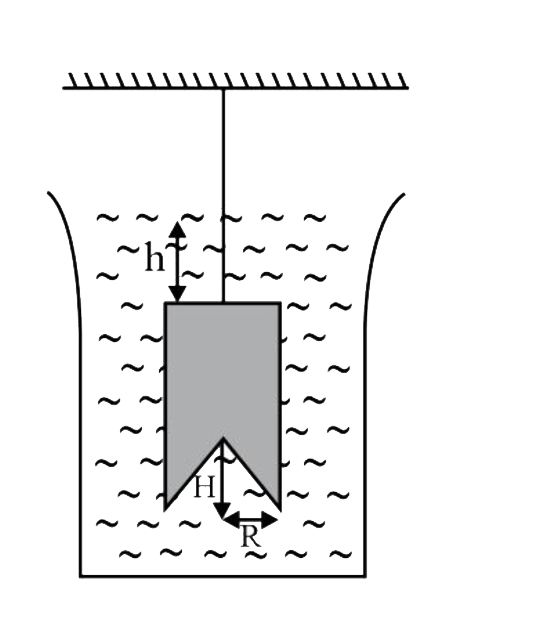 AMgBMg−VρgCMg+πR2hρgDρg(V+πR2h)
AMgBMg−VρgCMg+πR2hρgDρg(V+πR2h)
Curved surface area of a cylinder of radius h and height r is _______.
View SolutionThe sum of radius of the base and height of a cylinder is 37m. If the total surface area of the cylinder is 1628m2, find the curved surface area and volume of the cylinder
View SolutionA cylinder is inscribed in a sphere of radius r
What is the radius of the cylinder of maximum volume ?
View SolutionA sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is 4π r3 (b) 83π r3 (c) 2π r3 (d) 8π r3
View SolutionThe volumes of a sphere and a right circular cylinder having the same radius are equal. The ratio of the diameter of the sphere to the height of the cylinder is
View Solution
