A pipe of circular cross-section of inner radius r and outer radius 2r is bent into a semi circle as shown in the diagram. A fluid of density ρ=103kg/m3 is flowing through it. The breaking stress of the material of the pipe is 3×107n/m2. The maximum velocity with which the fluid can flow in the pipe is k×100m/s. find value of k.

2ρAv2=2F
σ=F3πr2=ρA3π
σ=ρv23
v=30m/s

Topper's Solved these Questions
Similar Questions
In the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
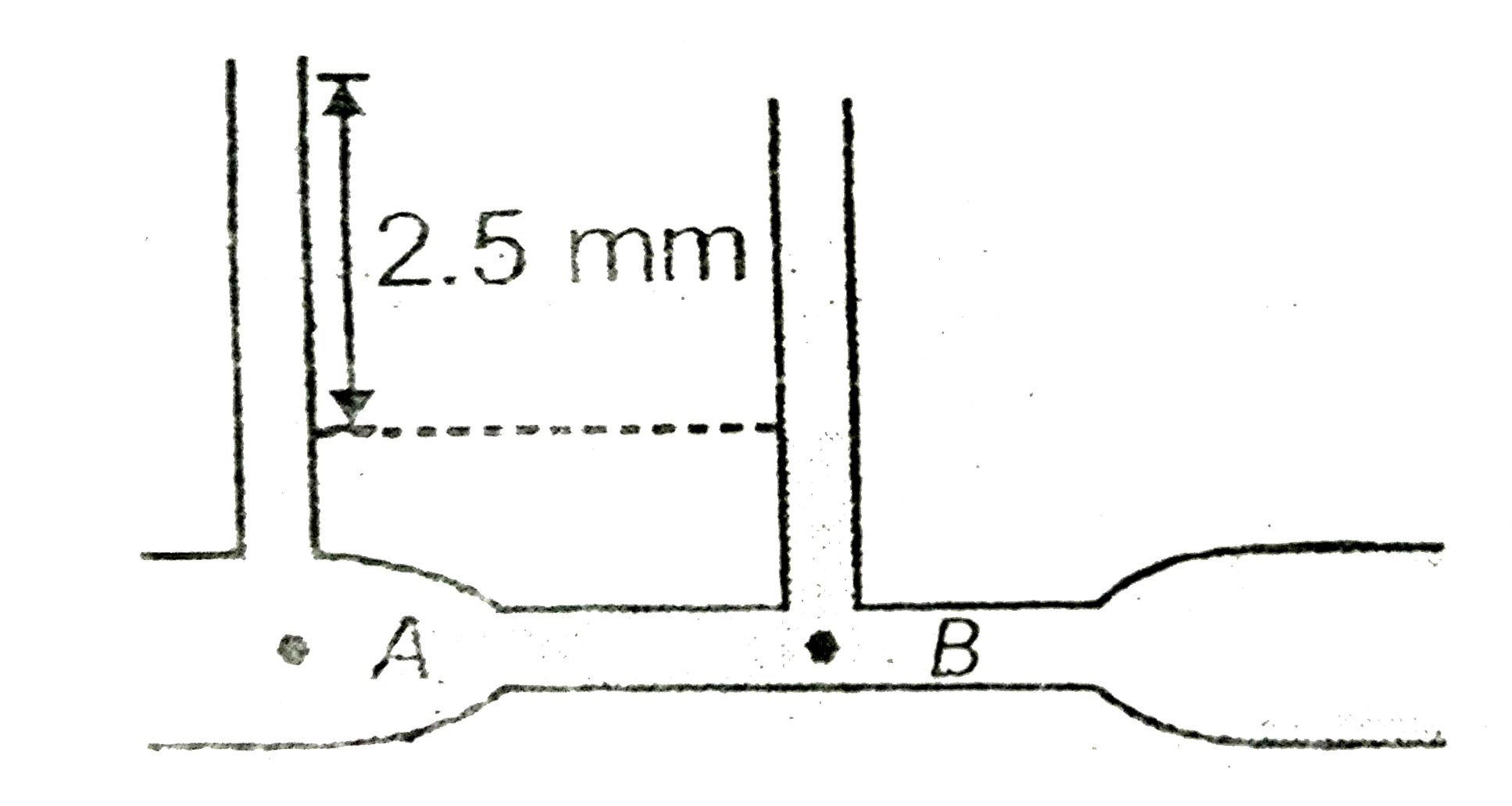
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?

View Solution
Knowledge Check
A small but heavy block of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. The area of the cross section of the wire is 10−6m2. The maximum angular velocity with which the block can be rotated in the horizontal circle is
A4rad/sB8rad/sC10rad/sD32rad/sA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
A8rad/secB4rad/secC2rad/secD1rad/secA body of mass 10 kg is attached to a wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross-section of wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
A4rad/sB8rad/sC16rad/sD32rad/s
A bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionThere is a conical pipe of radii of its two ends as 0.2m and 0.02m with 20 N/m2 as the pressure difference along its length. A liquid of density 1.00×103kg/m3 is flowing through the pipe. Calculate the rate of flow of liquid through the pipe.
View SolutionABC is a light pipe lying in a vertical plane and of cross sectional area 1cm2 whose small part is in ground to fix the pipe. An ideal fluid of density 104kg/m3 is being flown through the pipe by means of external agency. Length of BC can be neglected. The minimum vertical upward force required to pull out the pipe from ground is F=9N. What should be maximum velocity (in m/s) of the fluid so that pipe can not be pulled out from ground ?
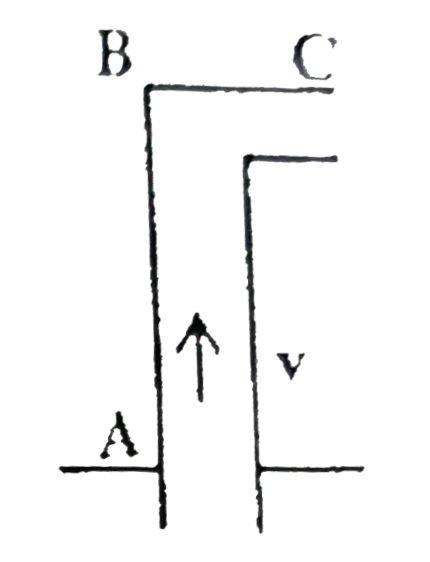
View SolutionABC is a light pipe lying in a vertical plane and of cross sectional area 1cm2 whose small part is in ground to fix the pipe. An ideal fluid of density 104kg/m3 is being flown through the pipe by means of external agency. Length of BC can be neglected. The minimum vertical upward force required to pull out the pipe from ground is F=9N. What should be maximum velocity (in m/s) of the fluid so that pipe can not be pulled out from ground ?

View Solution
