A cylindrical vessel of cross section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
2Aπa2√hg
√2Aπa2√hg
2√2Aπa2√hg
A√2πa2√hg
The correct Answer is:B
To find the time taken for a cylindrical vessel filled with water to empty through a hole at the bottom, we can follow these steps:
Step 1: Define the Variables
- Let A be the cross-sectional area of the cylindrical vessel.
- Let a be the radius of the hole at the bottom.
- Let h be the initial height of the water in the vessel.
- Let y be the height of the water at any time t.
Step 2: Write the Volume Discharge Equation
The volume of water that discharges through the hole in a small time dt can be expressed as:
dV=Ady
where dy is the change in height of the water.
Step 3: Use Torricelli's Law
According to Torricelli's law, the velocity V of water flowing out of the hole is given by:
V=√2gy
where g is the acceleration due to gravity.
Step 4: Write the Volume Flow Rate
The volume flow rate dV through the hole can also be expressed as:
dV=Area of the hole×Velocity×dt=πa2√2gydt
Step 5: Set the Two Volume Equations Equal
Since both expressions for dV represent the same volume of water discharged, we can set them equal:
Ady=πa2√2gydt
Step 6: Rearrange the Equation
Rearranging gives:
dy√y=−πa2A√2gdt
Step 7: Integrate Both Sides
Integrate both sides:
∫0hdy√y=−πa2A√2g∫t0dt
The left side integrates to:
−2(√y)∣∣∣0h=−2(0−√h)=2√h
The right side integrates to:
−πa2A√2gt
Step 8: Set the Integrals Equal
Setting the results of the integrals equal gives:
2√h=−πa2A√2gt
Step 9: Solve for Time t
Rearranging for t:
t=2A√hπa2√2g
Final Result
Thus, the time taken to empty the vessel is:
t=2Aπa2√h2g
- Let A be the cross-sectional area of the cylindrical vessel.
- Let a be the radius of the hole at the bottom.
- Let h be the initial height of the water in the vessel.
- Let y be the height of the water at any time t.
The volume of water that discharges through the hole in a small time dt can be expressed as:
dV=Ady
where dy is the change in height of the water.
According to Torricelli's law, the velocity V of water flowing out of the hole is given by:
V=√2gy
where g is the acceleration due to gravity.
The volume flow rate dV through the hole can also be expressed as:
dV=Area of the hole×Velocity×dt=πa2√2gydt
Since both expressions for dV represent the same volume of water discharged, we can set them equal:
Ady=πa2√2gydt
Rearranging gives:
dy√y=−πa2A√2gdt
Integrate both sides:
∫0hdy√y=−πa2A√2g∫t0dt
The left side integrates to:
−2(√y)∣∣∣0h=−2(0−√h)=2√h
The right side integrates to:
−πa2A√2gt
Setting the results of the integrals equal gives:
2√h=−πa2A√2gt
Rearranging for t:
t=2A√hπa2√2g
Thus, the time taken to empty the vessel is:
t=2Aπa2√h2g
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (JEE (Advanced) For IIT Entrance)
14 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (C. MCQ With More Than One Correct Answers)
12 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Competition File (B. MCQ (AIPMT/NEET & Other State Boards For Medical Entrance))
6 Videos
- MATHEMATICAL TOOLSBOOK - MODERN PUBLICATIONCHAPTER - MATHEMATICAL TOOLSEXERCISE - PRACTICE PROBLEMS (10)
12 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
Two identical cylindrical vessel with their bases at the same level each contain a liquid of density ρ. The height of the liquid in one vessel is h1 and in the other is h2 the area of either base is A. What is the work done by gravity is equalising the levels when the two vessels are connected?
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View Solution
Knowledge Check
A vessel of area of cross-section A has liquid to a height H . There is a hole at the bottom of vessel having area of cross-section a . The time taken to decrease the level from H1 to H2 will sec
AAa√2g[√H1−√H2]B√2ghC√2gh(H1−H2)DAa√g2[√H1−√H2A cylindrical vessel of area of cross-section A is filled with water to a height H. It has capillary tube of length l and radius r fitted horizontally at its bottom. If the coeffiecient of viscosity of water is η, then time required in which level will fall to a height H2 is (density of water is ρ)
Aη/r24Aρ1n(2)B4η/r4πgAρln(12)C8η/Aρπgr4ln(2)D4Hη/ρπgr4ln(2)Two cylindrical vessels of equal cross-sectional area. A contain water upto height h1 and h2. The vessels are interconnected so that the levels in them becomes equal. The work done by the force of gravity during the process is:
AzeroBρA(h1+h22)2gCρA(h1−h22)2gDρAh1h22g
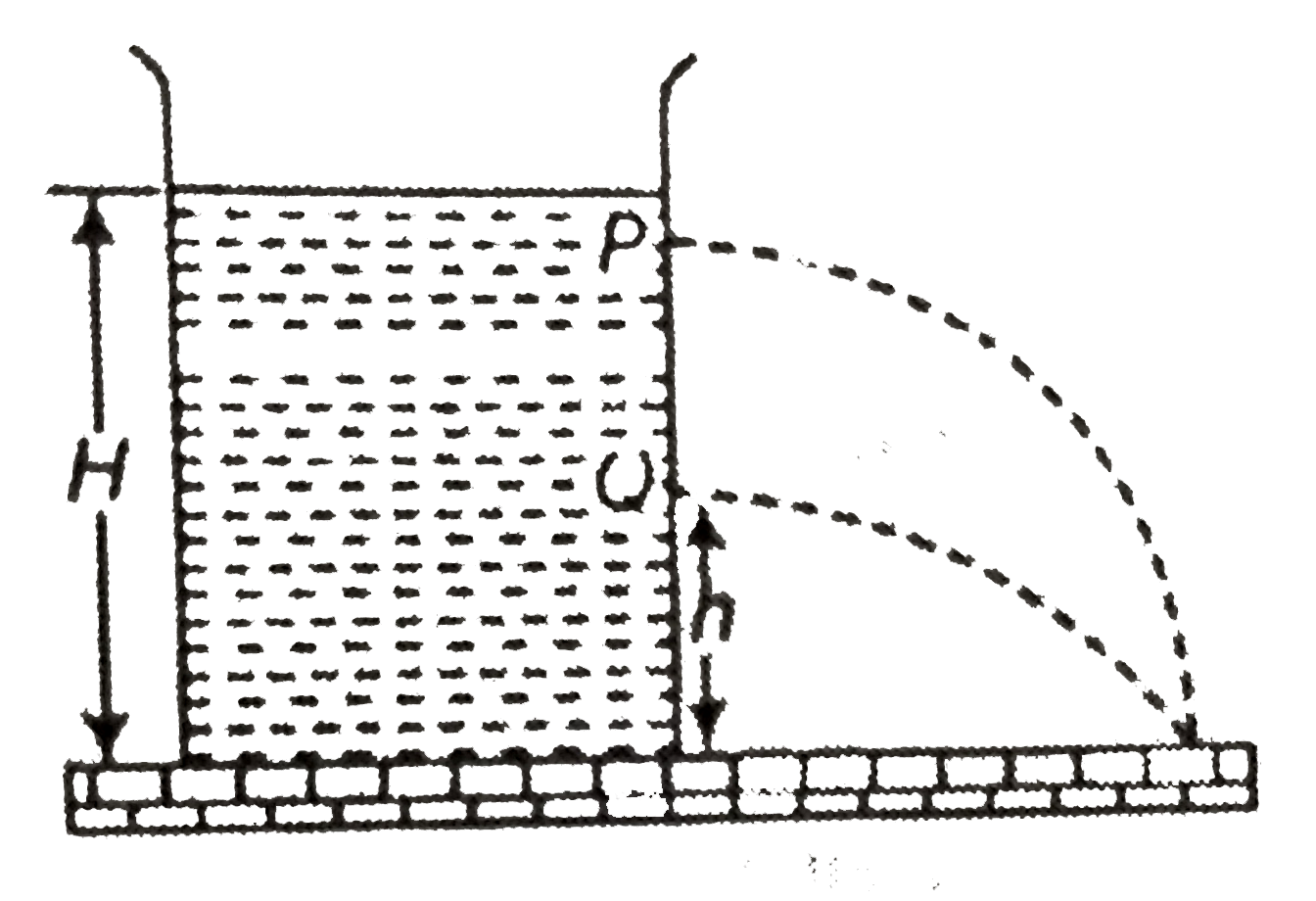
A cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
View SolutionA cylindrical vessel of uniform cross-section contains liquid upto the height' H’ . At a depth H=H2 below the free surface of the liquid there is an orifice. Using Bernoulli's theorem, find the velocity of efflux of liquid.
View SolutionA vessel of 100cm2 cross sectional area contains water. The mass of water is 2 kg. Find the pressure acting on the bottom surface.
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View Solution
