The temperature difference between two ends of a 2 m long bar A is 40∘C and that between a 3 m long bar B of same area is 60∘C . If the rate of conduction of heat in two bars is same, calculate the ratio of coefficients of thermal conductivity of two bars.
To solve the problem, we need to use the formula for the rate of heat conduction through a material, which is given by Fourier's law of heat conduction:
Q=k⋅A⋅ΔTL
Where:
- Q = rate of heat transfer
- k = coefficient of thermal conductivity
- A = cross-sectional area of the bar
- ΔT = temperature difference between the two ends
- L = length of the bar
Given:
- For bar A:
- Length LA=2m
- Temperature difference ΔTA=40∘C
- For bar B:
- Length LB=3m
- Temperature difference ΔTB=60∘C
Since the rate of conduction of heat in both bars is the same, we can set the equations for both bars equal to each other:
kA⋅A⋅ΔTALA=kB⋅A⋅ΔTBLB
Step 1: Cancel the cross-sectional area A from both sides of the equation, as it is the same for both bars.
kA⋅ΔTALA=kB⋅ΔTBLB
Step 2: Substitute the known values into the equation:
kA⋅402=kB⋅603
Step 3: Simplify both sides:
20kA=20kB
Step 4: Divide both sides by 20:
kA=kB
Step 5: Therefore, the ratio of the coefficients of thermal conductivity of the two bars is:
kAkB=1
Final Answer: The ratio of coefficients of thermal conductivity of the two bars is 1:1.
- Q = rate of heat transfer
- k = coefficient of thermal conductivity
- A = cross-sectional area of the bar
- ΔT = temperature difference between the two ends
- L = length of the bar
- For bar A:
- Length LA=2m
- Temperature difference ΔTA=40∘C
- For bar B:
- Length LB=3m
- Temperature difference ΔTB=60∘C
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CONCEPTUAL QUESTIONS
16 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - TOUGH AND TRICKY PROBLEM
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
The temperature difference between the two ends of a bar 1.0 m long is 50∘C and that for the other bar 1.25 m long 75∘C. Both the bars have same area of cross-section. If the rates of conduction of heat in the two bars are the same, find the ratio of the coefficients of thermal conductivity of the materials of the two bars.
View SolutionThe temperature difference between the two ends of a bar 1.0 m long is 50∘C and that for the other bar 1.25 m long 75∘C. Both the bars have same area of cross-section. If the rates of conduction of heat in the two bars are the same, find the ratio of the coefficients of thermal conductivity of the materials of the two bars.
View Solution
Knowledge Check
A rod of 40 cm in length and temperature difference of 80∘C at its two ends. Another rod B of length 60cm and of temperature difference 90∘C, having the same area of cross-section. If the rate of flow of heat is the same, then the ratio of their thermal conductivities will be
A3:4B4:3C1:2D2:1The angle θ between two non-zero vectors ¯aand¯b is given by cosθ =….
A¯a.¯b|¯a|∣∣¯b∣∣B¯a.¯bC|¯a|∣∣¯b∣∣D|¯a|∣∣¯b∣∣¯a.¯b
A steel bar 10.0 cm long is welded end to end to a copper bae 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K

View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the juction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
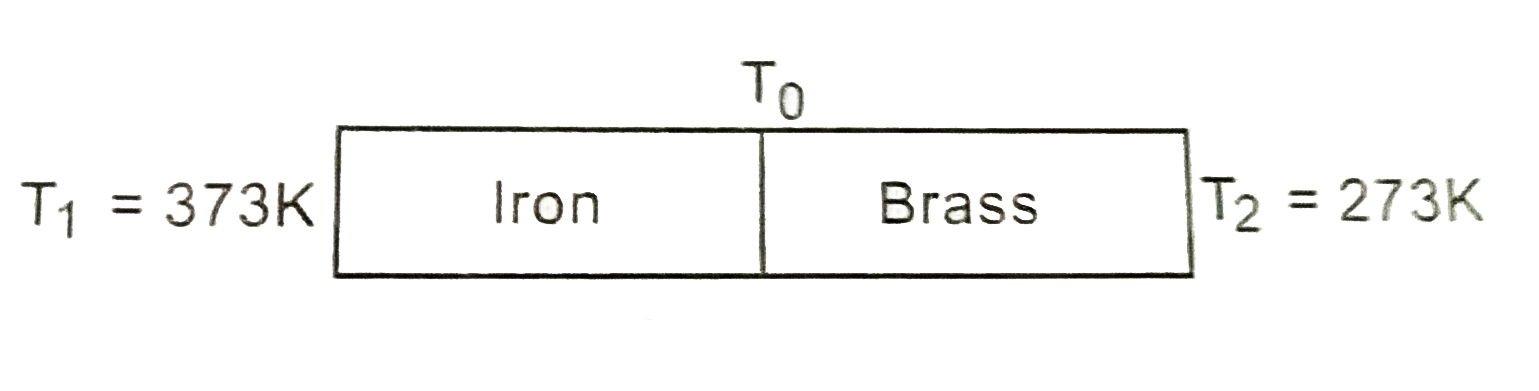 .
.
View SolutionThe ratio of the areas of cross-section of two rods of different materials is 1:2, and the ratio of the thermal conductivities of their materials is 4:3. On keeping equal temperature-difference between the ends of these rods, the rate of conduction of heat are equal. Determine the ratio of the lengths of the rods.
View SolutionIn fig, two bars of the same metal are connected. The length of the first bar is half of that of the second, but the cross-sectional area is double. What is the temperature of the junction of the bars ?

View SolutionThe ends of a metallic bar are maintained at different temperature and there is no loss/gain of heat from the sides of the bar due to conduction or radiation. In the steady state the temperature variation along the length of the bar is a shown in the figure what do you think about the cross sectional area of the bar?
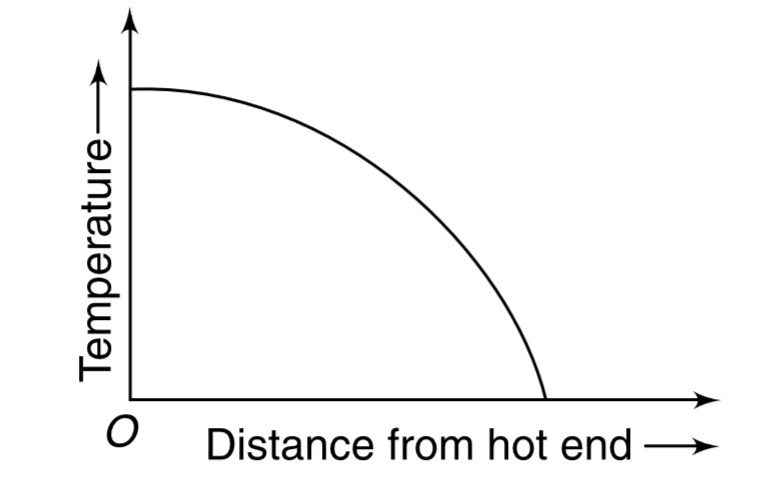
View Solution
