The temperature difference between the two ends of a bar 1.0 m long is 50∘C and that for the other bar 1.25 m long 75∘C. Both the bars have same area of cross-section. If the rates of conduction of heat in the two bars are the same, find the ratio of the coefficients of thermal conductivity of the materials of the two bars.
To find the ratio of the coefficients of thermal conductivity of the materials of the two bars, we can use the formula for the rate of heat conduction through a material, which is given by:
Q=K⋅A⋅(T1−T2)L
where:
- Q is the rate of heat transfer,
- K is the coefficient of thermal conductivity,
- A is the area of cross-section,
- T1−T2 is the temperature difference,
- L is the length of the bar.
Given the problem, we have two bars with the following parameters:
Bar 1:
- Length L1=1.0m
- Temperature difference ΔT1=50∘C
Bar 2:
- Length L2=1.25m
- Temperature difference ΔT2=75∘C
Since the rates of conduction of heat in the two bars are the same, we can set up the equation:
K1⋅A⋅ΔT1L1=K2⋅A⋅ΔT2L2
Since the area A is the same for both bars, we can cancel A from both sides:
K1⋅ΔT1L1=K2⋅ΔT2L2
Now, rearranging the equation gives us:
K1K2=ΔT2⋅L1ΔT1⋅L2
Substituting the known values:
K1K2=75⋅1.050⋅1.25
Calculating the right-hand side:
1. Calculate the numerator: 75⋅1.0=75
2. Calculate the denominator: 50⋅1.25=62.5
Now we have:
K1K2=7562.5
To simplify 7562.5:
7562.5=75÷12.562.5÷12.5=65
Thus, the ratio of the coefficients of thermal conductivity of the two bars is:
K1K2=65
Final Answer:
The ratio of the coefficients of thermal conductivity of the materials of the two bars is 65.
---
- Q is the rate of heat transfer,
- K is the coefficient of thermal conductivity,
- A is the area of cross-section,
- T1−T2 is the temperature difference,
- L is the length of the bar.
- Length L1=1.0m
- Temperature difference ΔT1=50∘C
- Length L2=1.25m
- Temperature difference ΔT2=75∘C
2. Calculate the denominator: 50⋅1.25=62.5
The ratio of the coefficients of thermal conductivity of the materials of the two bars is 65.
Topper's Solved these Questions
- Thermal Properties of MatterBOOK - SL ARORACHAPTER - Thermal Properties of MatterEXERCISE - Exercise
449 Videos
- System of particles & rotational MotionBOOK - SL ARORACHAPTER - System of particles & rotational MotionEXERCISE - EXERCISE
353 Videos
- THERMODYNAMICSBOOK - SL ARORACHAPTER - THERMODYNAMICSEXERCISE - Exercise
342 Videos
Similar Questions
The temperature difference between two ends of a 2 m long bar A is 40∘C and that between a 3 m long bar B of same area is 60∘C . If the rate of conduction of heat in two bars is same, calculate the ratio of coefficients of thermal conductivity of two bars.
View SolutionTwo bar of identical dimensions are kept as shown in figure. If K1 and K2are their coefficients of thermal conductivities, then equivalent K

View Solution
Knowledge Check
A rod of 40 cm in length and temperature difference of 80∘C at its two ends. Another rod B of length 60cm and of temperature difference 90∘C, having the same area of cross-section. If the rate of flow of heat is the same, then the ratio of their thermal conductivities will be
A3:4B4:3C1:2D2:1Two rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
AA1A2=L1K2BA1A2=K2K1CA1A2=K1K2Dplaced in hot oilThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
A4:5B9:1C1:9D5:4
In fig, two bars of the same metal are connected. The length of the first bar is half of that of the second, but the cross-sectional area is double. What is the temperature of the junction of the bars ?

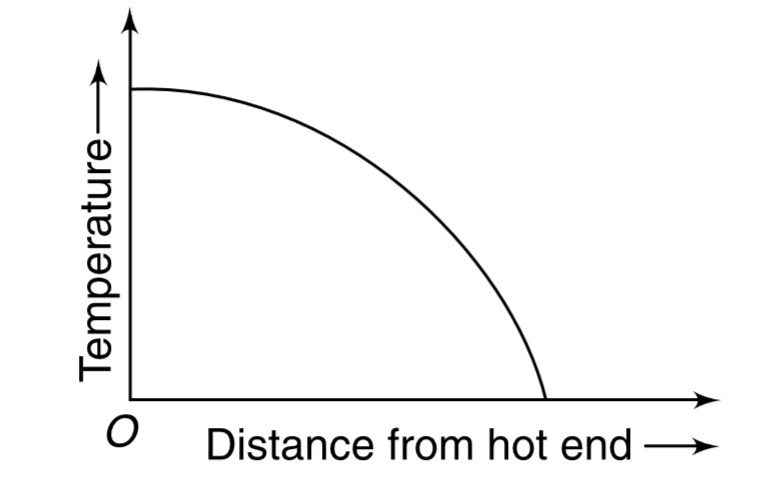
View SolutionThe ends of a metallic bar are maintained at different temperature and there is no loss/gain of heat from the sides of the bar due to conduction or radiation. In the steady state the temperature variation along the length of the bar is a shown in the figure what do you think about the cross sectional area of the bar?
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionThe ratio of the areas of cross-section of two rods of different materials is 1:2, and the ratio of the thermal conductivities of their materials is 4:3. On keeping equal temperature-difference between the ends of these rods, the rate of conduction of heat are equal. Determine the ratio of the lengths of the rods.
View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View Solution
