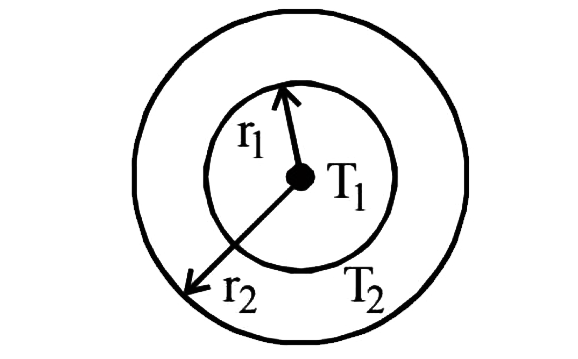
The figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
(r2−r1)/r1r2
ln(r2r1)
r1r2(r2−r1)
(r2−r1)
The correct Answer is:C
Heat blowing radially through the surface area of shell is not constant. Thermal resistance is given by
R=LKA, K is thermal conductivity
dQdt=KAdTL=1R(T1−T2) ...(i)
Let us consider a small spherical element of thickness dr at a distance r from the centre of the shell dR=drK4πr2

dQdt=(T1−T2)4πr1r2K(r2−r1)
∴dQdt∝r1r2(r2−r1)
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE ADVANCED FOR IIT ENTRANCE )
9 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((C ) MULTIPLE CHOICE QUESTION WITH MORE THAN ONE CORRECT ANSWER)
11 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) AIMPMT/NEET AND OTHER STATE BOARDS FOR MEDICAL ENTRANCE)
18 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Solve the foregoing problem for the case of two concentric spheres of radii R1 and R2 and temperatures T1 and T2.
View SolutionFig, shows a system of two concentric spheres of radii r1 andr2 and kept at temperature T1 and T2(T1>T2) respectively. Find the expression for radial rate of flow of heat through the substance.

View Solution
Knowledge Check
A system consists of two concentric spherical shells of radii a and b(b>a) maintained at temperature T1 and T2 respectively. The radial rate of flow of heat through substance between the two concentric spherical shells is proportional to
Ab - aBabb−aCloge(ba)Db−aabTwo spheres of the same material having radii r and 4r and temperature 2T0 and T0 respectively. The ratio of rate of radiation of energy by the sphere is
A1:1B1:2C2:1D3:1Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1
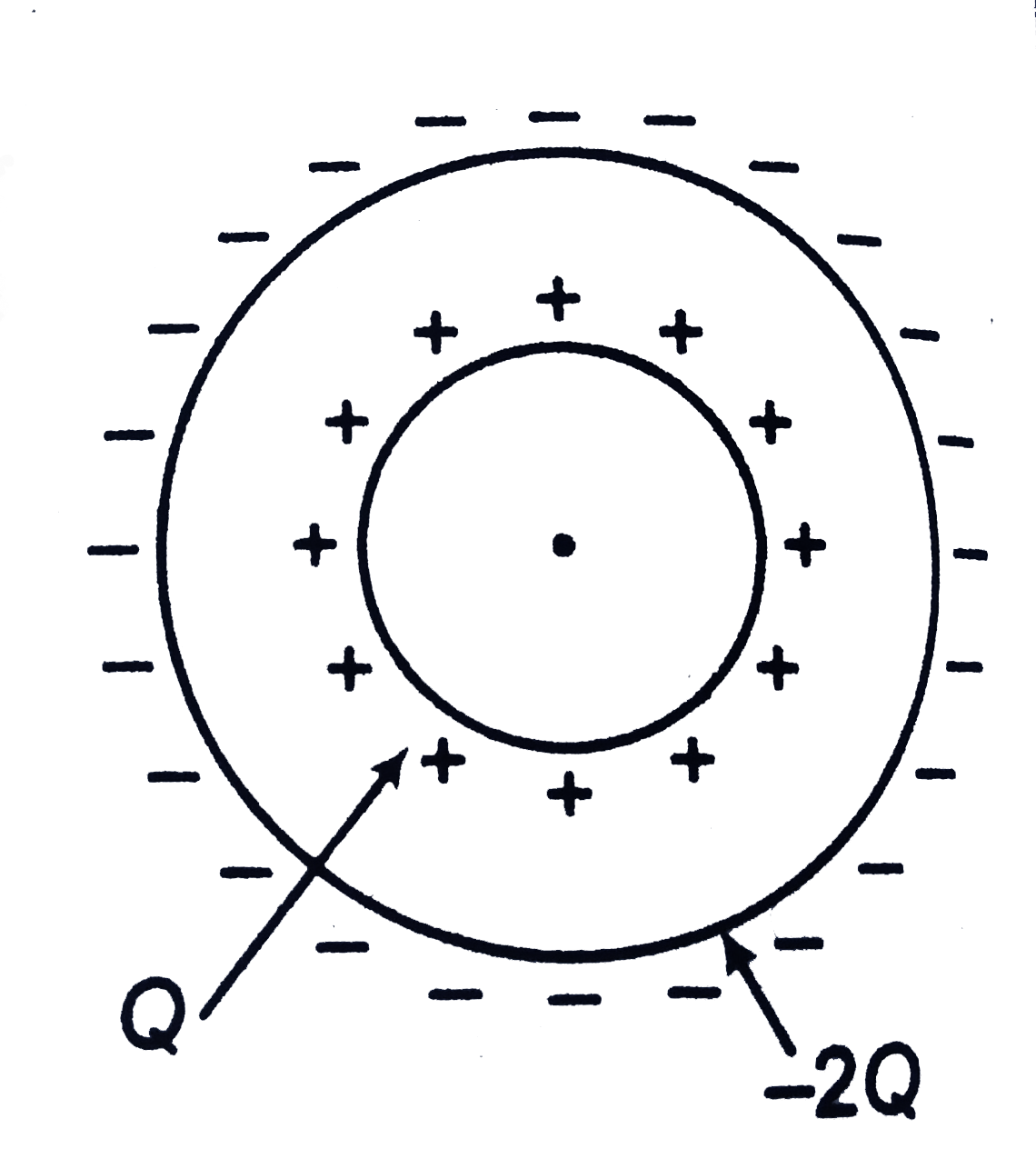
Two concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionTwo spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionThe capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionTwo conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
View Solution