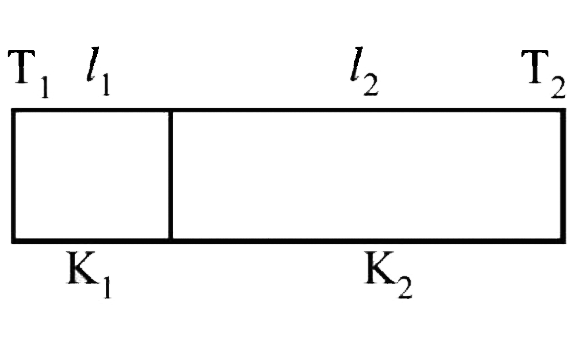
One end of a thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two sections of length $l_{1} and l_{2}$ and thermal conductivities $K_{1} and K_{2}$ respectively. The temperature at the interface of the two section is

A

$(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2}) / (k_{1} l_{1} + k_{2} l_{2})$

B

$(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2}) / (k_{2} l_{1} + k_{1} l_{2})$

C

$(k_{1} l_{2} T_{1} + k_{2} l_{1} T_{2}) / (k_{1} l_{2} + k_{2} l_{1})$

D

$(k_{1} l_{1} T_{1} + k_{2} l_{2} T_{2}) / (k_{1} l_{1} + k_{2} l_{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As both rods are connected in series, the rate of flow of heat is same. Let T be the temperature at the junction of rods,
$A \frac{(T_{1} - T) k_{1}}{l_{1}} = A \frac{(T - T_{2}) k_{2}}{l_{2}}$
$T = \frac{T_{1} k_{1} l_{2} + T_{2} k_{2} l_{1}}{k_{1} l_{2} + k_{2} l_{1}}$

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
One end of thermally insulated rod is kept at a temperature $T_{1}$ and the other at $T_{2}$ . The rod is composed of two section of length $l_{1}$ and $l_{2}$ thermal conductivities $k_{1}$ and $k_{2}$ respectively. The temerature at the interface of two section is
A $\frac{(k_{1} l_{1} T_{1} + k_{2} l_{2} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
B $\frac{(k_{2} l_{2} T_{1} + k_{1} l_{1} T_{2})}{(k_{1} l_{1} + k_{2} l_{2})}$
C $\frac{(k_{2} l_{1} T_{1} + k_{1} l_{2} T_{2})}{(k_{2} l_{1} + k_{1} l_{2})}$
D $\frac{(k_{1} l_{2} T_{1} + k_{2} l_{1} T_{2})}{(k_{1} l_{2} + k_{2} l_{1})}$
Question 2 - Select One
Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is
A $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
B $(K_{1} + K_{2})$
C $\frac{K_{1} + K_{2}}{2}$
D $\sqrt{K_{1} K_{2}}$
Question 3 - Select One
Two rods of the same length and diameter having thermal conductivities $K_{1}$ and $K_{2}$ are joined in parallel. The equivalent thermal conductivity of combination is
A $\frac{K_{1} K_{2}}{K_{1} + K_{2}}$
B $(K_{1} + K_{2})$
C $\frac{K_{1} + K_{2}}{2}$
D $\sqrt{K_{1} K_{2}}$

MODERN PUBLICATION-THERMAL PROPERTIES OF MATTER-COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION FROM CPMPETITIVE EXAMINATION ) JEE MAIN AND OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)

Home
Ask Doubt
Profile