Two small spheres each of mass 'm' kg and charge q coulomb are suspended from a point by insulating threads each of 1 metre length, but of negliglible mass. If is the angle which each string makes with the verticle vertical when equilbrium has been reached, show that
The correct Answer is:
To solve the problem, we need to analyze the forces acting on each sphere when they are in equilibrium. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have two small spheres, each with mass m and charge q, suspended by insulating threads of length l. When in equilibrium, each thread makes an angle θ with the vertical.
Step 2: Identify Forces Acting on Each Sphere
Each sphere experiences:
- Gravitational force Fg=mg acting downwards.
- Tension T in the thread acting along the thread.
- Electrostatic force Fe due to the repulsion between the two charged spheres.
Step 3: Resolve the Tension Force
The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
Step 4: Apply Equilibrium Conditions
In equilibrium:
1. The vertical forces must balance:
Tcosθ=mg(1)
2. The horizontal forces must balance (the electrostatic force equals the horizontal component of tension):
Tsinθ=Fe(2)
Step 5: Calculate the Electrostatic Force
The electrostatic force Fe between the two charges is given by Coulomb's law:
Fe=kq2r2
where k=14πϵ0 and r is the distance between the two spheres.
Step 6: Determine the Distance r
Using geometry, the distance r between the two spheres can be expressed as:
r=2lsinθ
Step 7: Substitute r into the Electrostatic Force Equation
Substituting r into the expression for Fe:
Fe=kq2(2lsinθ)2=kq24l2sin2θ
Step 8: Substitute Fe into Equation (2)
From Equation (2):
Tsinθ=kq24l2sin2θ
Step 9: Substitute T from Equation (1)
From Equation (1), we can express T:
T=mgcosθ
Substituting this into the equation gives:
mgcosθsinθ=kq24l2sin2θ
Step 10: Rearranging the Equation
Now, rearranging the equation:
mgtanθ=kq24l2sin2θ
Multiplying both sides by 4l2sin2θ:
4mgl2sin2θtanθ=kq2
Step 11: Substitute k
Substituting k=14πϵ0:
4mgl2sin2θtanθ=14πϵ0q2
Step 12: Final Rearrangement
Rearranging gives:
q2=4mgl2sin2θtanθ(4πϵ0)
Conclusion
Thus, we have shown that:
q2=4mgl2sin2θtanθ(4πϵ0)
We have two small spheres, each with mass m and charge q, suspended by insulating threads of length l. When in equilibrium, each thread makes an angle θ with the vertical.
Each sphere experiences:
- Gravitational force Fg=mg acting downwards.
- Tension T in the thread acting along the thread.
- Electrostatic force Fe due to the repulsion between the two charged spheres.
The tension T can be resolved into two components:
- Vertical component: Tcosθ
- Horizontal component: Tsinθ
In equilibrium:
1. The vertical forces must balance:
Tcosθ=mg(1)
2. The horizontal forces must balance (the electrostatic force equals the horizontal component of tension):
Tsinθ=Fe(2)
The electrostatic force Fe between the two charges is given by Coulomb's law:
Fe=kq2r2
where k=14πϵ0 and r is the distance between the two spheres.
Using geometry, the distance r between the two spheres can be expressed as:
r=2lsinθ
Substituting r into the expression for Fe:
Fe=kq2(2lsinθ)2=kq24l2sin2θ
From Equation (2):
Tsinθ=kq24l2sin2θ
From Equation (1), we can express T:
T=mgcosθ
Substituting this into the equation gives:
mgcosθsinθ=kq24l2sin2θ
Now, rearranging the equation:
mgtanθ=kq24l2sin2θ
Multiplying both sides by 4l2sin2θ:
4mgl2sin2θtanθ=kq2
Substituting k=14πϵ0:
4mgl2sin2θtanθ=14πϵ0q2
Rearranging gives:
q2=4mgl2sin2θtanθ(4πϵ0)
Thus, we have shown that:
q2=4mgl2sin2θtanθ(4πϵ0)
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - FILL IN THE BLANKS8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - PROBLEMS FOR PRACTICE8videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - VALUE BASED QUESTIONS7videos
ELECTROSTATICS
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - Fill in the Blanks1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)2videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
2 small spheres each of mass m and carrying +q coulomb, are suspended by massles insulating threads, each of length l. Prove that q2=(4mgl2sin2θtanθ)4πε0, where θ is angle made of strings with the vertical at equilibrium.
View SolutionTwo idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
Ax=(q2l2πε0mg)1/2Bx=(q2l2πε0mg)1/3Cx=(q2l22πε0m2g)1/3Dx=(q2l22πε0m2g2)1/3 - Question 2 - Select One
Two identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
AKq2l2+2mgBKq24l2+2mgCKq2l2DKq24l2
Two identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
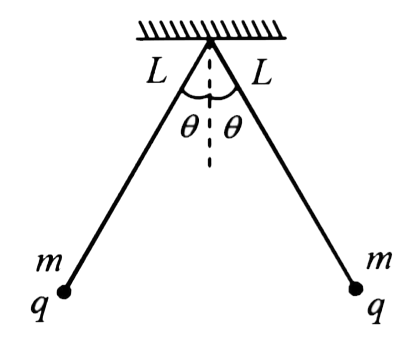 View Solution
View SolutionTwo small spheres each of mass m are suspended from a common point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.28m. If =g10ms−2, what is the charge on each sphere?
View SolutionTwo small spheres each of mass 10−6 kg are suspended from a point by silkk threads 50cm long. They are equally chareged and repel each other to a distance 20cm apart. Calculate charege on each Take g=9.8ms−2.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution

