Two charges of 2 mC and 8 mC are kept at (2 m,0) and (7 m, 0) respectively. At what position, a third charge Q should be kept so that all the three charges are in equilibrium. Also calculate the magnitude of charge Q.
To solve the problem of finding the position and magnitude of the charge Q such that all three charges are in equilibrium, we can follow these steps:
Step 1: Understand the Problem
We have two charges:
- Q1=2mC located at (2m,0)
- Q2=8mC located at (7m,0)
We need to find the position x of a third charge Q such that the net force acting on each charge is zero.
Step 2: Set Up the Forces
The forces acting on Q1 due to Q2 and Q must balance each other. The force between two charges is given by Coulomb's law:
F=k|Q1Q2|r2
Where k is Coulomb's constant.
Step 3: Define the Position of Charge Q
Let the position of charge Q be x meters from Q1. Therefore, the distance from Q1 to Q is x and from Q2 to Q is (5−x) meters (since Q2 is at 7m and Q1 is at 2m).
Step 4: Write the Force Equations
1. The force on Q1 due to Q2:
F12=kQ1Q2(5)2
2. The force on Q1 due to Q:
F1Q=kQ1Qx2
For equilibrium, these forces must be equal:
kQ1Q2(5)2=kQ1Qx2
Step 5: Cancel Out Common Terms
Since k and Q1 are common on both sides, we can simplify:
Q225=Qx2
Thus,
Q=Q2⋅x225
Step 6: Write the Force Equation for Q2
Similarly, for charge Q2:
FQ2Q=kQ2Q(5−x)2
Setting this equal to the force FQ2Q1:
kQ2Q1(5)2=kQ2Q(5−x)2
Cancelling k and Q2:
Q125=Q(5−x)2
Thus,
Q=Q1⋅(5−x)225
Step 7: Equate the Two Expressions for Q
Now we have two expressions for Q:
Q2⋅x225=Q1⋅(5−x)225
Removing the common factor of 125:
Q2⋅x2=Q1⋅(5−x)2
Step 8: Substitute Values
Substituting Q1=2mC and Q2=8mC:
8x2=2(5−x)2
Expanding and simplifying:
8x2=2(25−10x+x2)
8x2=50−20x+2x2
6x2+20x−50=0
Step 9: Solve the Quadratic Equation
Using the quadratic formula:
x=−b±√b2−4ac2a
Where a=6,b=20,c=−50:
x=−20±√202−4⋅6⋅(−50)2⋅6
x=−20±√400+120012
x=−20±√160012
x=−20±4012
Calculating the two possible values:
1. x=2012=53m
2. x=−6012 (not valid since distance cannot be negative)
Step 10: Calculate the Magnitude of Charge Q
Substituting x=53 back into either equation for Q:
Q=8⋅(53)225=8⋅25925=89mC
Final Answer
The position of charge Q is 53m from Q1 and the magnitude of charge Q is 89mC.
We have two charges:
- Q1=2mC located at (2m,0)
- Q2=8mC located at (7m,0)
The forces acting on Q1 due to Q2 and Q must balance each other. The force between two charges is given by Coulomb's law:
F=k|Q1Q2|r2
Where k is Coulomb's constant.
Let the position of charge Q be x meters from Q1. Therefore, the distance from Q1 to Q is x and from Q2 to Q is (5−x) meters (since Q2 is at 7m and Q1 is at 2m).
1. The force on Q1 due to Q2:
F12=kQ1Q2(5)2
2. The force on Q1 due to Q:
F1Q=kQ1Qx2
kQ1Q2(5)2=kQ1Qx2
Since k and Q1 are common on both sides, we can simplify:
Q225=Qx2
Thus,
Q=Q2⋅x225
Similarly, for charge Q2:
FQ2Q=kQ2Q(5−x)2
Setting this equal to the force FQ2Q1:
kQ2Q1(5)2=kQ2Q(5−x)2
Cancelling k and Q2:
Q125=Q(5−x)2
Thus,
Q=Q1⋅(5−x)225
Now we have two expressions for Q:
Q2⋅x225=Q1⋅(5−x)225
Removing the common factor of 125:
Q2⋅x2=Q1⋅(5−x)2
Substituting Q1=2mC and Q2=8mC:
8x2=2(5−x)2
Expanding and simplifying:
8x2=2(25−10x+x2)
8x2=50−20x+2x2
6x2+20x−50=0
Using the quadratic formula:
x=−b±√b2−4ac2a
Where a=6,b=20,c=−50:
x=−20±√202−4⋅6⋅(−50)2⋅6
x=−20±√400+120012
x=−20±√160012
x=−20±4012
Calculating the two possible values:
1. x=2012=53m
2. x=−6012 (not valid since distance cannot be negative)
Substituting x=53 back into either equation for Q:
Q=8⋅(53)225=8⋅25925=89mC
The position of charge Q is 53m from Q1 and the magnitude of charge Q is 89mC.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions51videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Tough & Tricky Problems20videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test15videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two point charges of, 1 μC and -1 μC are kept at (-2 m, 0) and (2 m, 0) respectively. Calculate the electric field at point (0, 5 m).
View SolutionTwo idential point charges Q are kept at a distance r from each other. A third point charge is placed on the line joing the above two charges such that all the three charges are in equilibrium. The third charge
(a) should be of magnitude q=………..
(b) should be of sign .......
(c ) should be placed ........ .View Solution
Knowledge Check
- Question 1 - Select One
Two point charges +4q and +q are placed at a distance L apart. A third charge Q is so placed that all the three charges are in equilibrium. Then location. And magnitude of the third charge will be
AAt a distance L3 from +4q charge, 4q9BAt a distance L3 from +4q charge −4q9CAt a distance 2L3 from +4q charge −4q9DAt a distance 2L3 from +q charge 4q9 - Question 2 - Select One
Two point charges +q and −q are placed a distance x apart. A third charge is so placed that al the three charges are in equilibrium. Then
Auknknown charge is −4q/9Bunknown charge is −9q/4Cit should be at (x/3)from smaller chargge between themDnone of these - Question 3 - Select One
Two point electric charges of value q and 2q are kept at a distance d apart from each other in air. A third charge Q is to be kept along the same line in such a way that the net force action on q and 2q is zero. Calculate the position of charge Q in terms of q and d.
Ad√2−1Bd√2+1Cd√3+1Dd√3−1
Two charges +q and -q are kept at (−x1,0)and(x1,0) respectively in the x-y plane. Find the magnitude and direction of the net electric field at the origin (0,0)
View SolutionTwo point charges 8 μC and −8μC are kept at points (-2cm, 0) and (2cm, 0), respectively. Calculate the electric potential at points (0, 7cm) and (4cm, 0).
View Solution(a) Two point charges Q and 16Q are fixed at separation d. Where should a third point charge be placed between them so that it experiences no force I.e. in equilibrium ?
(b) In the previous problem , if we replace Q by −Q , where should the third charge be placed on the joining the charges so that it is equilibrium ?
(c ) Three point charges Q,q and Q are placed at x=0,x=d/2 and x=d. Find q in terms of Q so that all charges are in equilibrium.
(d) Two point charges 9Q and 25Q are placed at separation d. Where should a third charge q be placed between them so that all charges are in equilibrium ? Also find the value of q and its nature.View SolutionThree point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
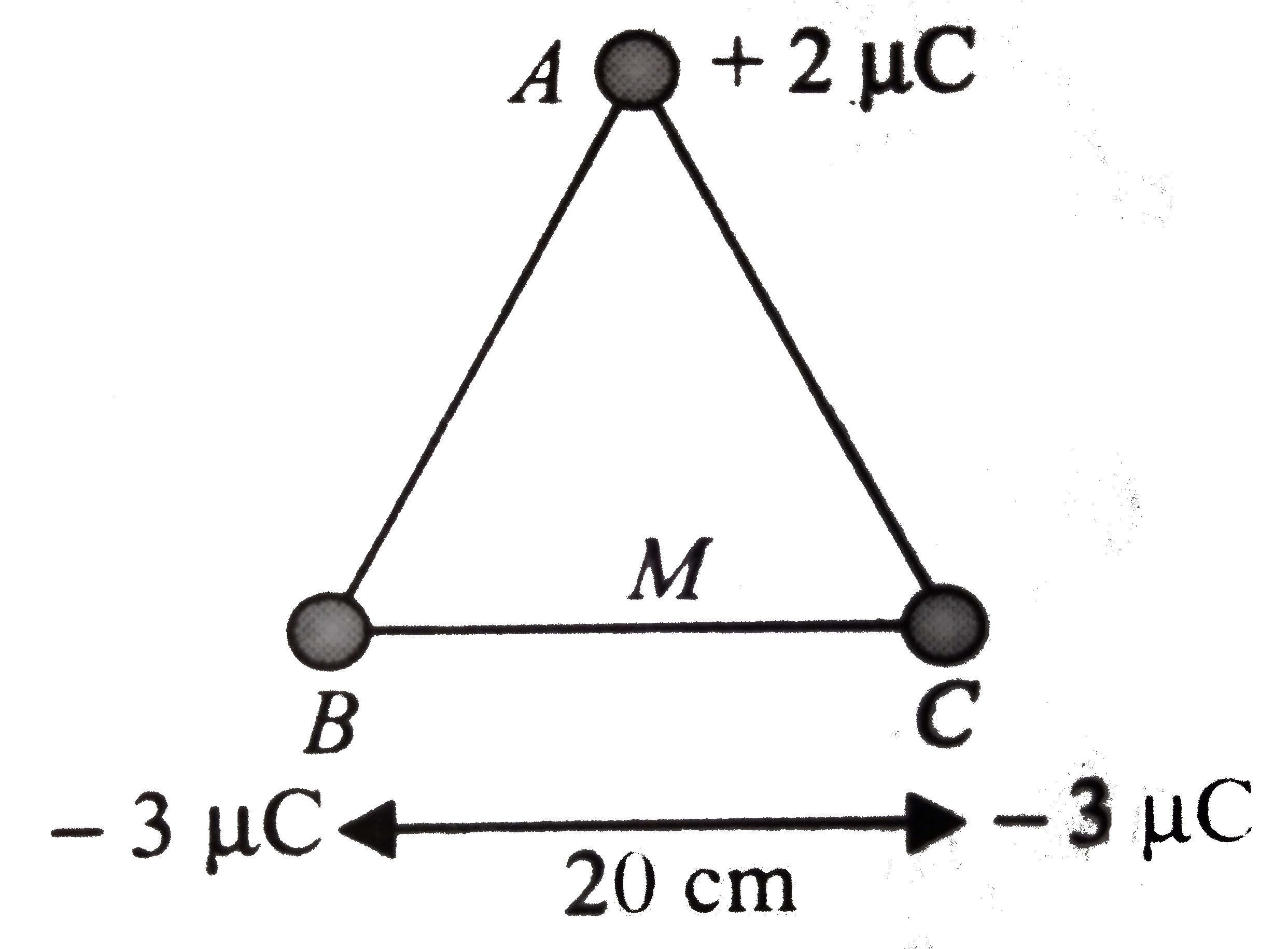 View Solution
View SolutionTwo free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then magnitude of third charge and postion,
View Solution

