Positive charge Q is uniformly distributed across a thin rod of length L. The rod is then bent in the form of a semicircle. What will be the electric potential at the centre of curvature of semicircle formed?
To find the electric potential at the center of curvature of a semicircle formed by a thin rod of length L with a uniformly distributed positive charge Q, we can follow these steps:
Step 1: Determine the Radius of the Semicircle
The length of the rod L when bent into a semicircle corresponds to the semicircular arc length. The length of a semicircle is given by:
L=πR
where R is the radius of the semicircle. From this, we can express R as:
R=Lπ
Step 2: Define Linear Charge Density
The linear charge density λ (charge per unit length) of the rod can be defined as:
λ=QL
Step 3: Consider an Element of Charge
Consider a small element of length dx on the semicircle, which will have a small charge dq:
dq=λdx=QLdx
Step 4: Electric Potential Contribution from dq
The electric potential dV at the center of curvature due to the small charge dq is given by the formula:
dV=kdqr
where k=14πϵ0 is Coulomb's constant and r is the distance from the charge element to the point where we are calculating the potential (which is the radius R of the semicircle). Thus:
dV=kdqR=kR⋅QLdx
Step 5: Integrate to Find Total Electric Potential
To find the total electric potential V at the center of curvature, we need to integrate dV over the entire semicircle. The limits of integration will be from 0 to L:
V=∫L0dV=∫L0kR⋅QLdx
Since R=Lπ, we substitute this into the equation:
V=∫L0k⋅QLLπdx=∫L0k⋅Q⋅πL2dx
Step 6: Evaluate the Integral
The integral simplifies to:
V=k⋅Q⋅πL2∫L0dx=k⋅Q⋅πL2⋅L=k⋅Q⋅πL
Step 7: Substitute k and Simplify
Substituting k=14πϵ0:
V=14πϵ0⋅Q⋅πL=Q4ϵ0L
Final Result
Thus, the electric potential at the center of curvature of the semicircle is:
V=Q4πϵ0L
The length of the rod L when bent into a semicircle corresponds to the semicircular arc length. The length of a semicircle is given by:
The linear charge density λ (charge per unit length) of the rod can be defined as:
Consider a small element of length dx on the semicircle, which will have a small charge dq:
The electric potential dV at the center of curvature due to the small charge dq is given by the formula:
To find the total electric potential V at the center of curvature, we need to integrate dV over the entire semicircle. The limits of integration will be from 0 to L:
The integral simplifies to:
Substituting k=14πϵ0:
Thus, the electric potential at the center of curvature of the semicircle is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 5
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
A positive charge Q is uniformly distributed across a rod of length L. The rod is then bent in the form of a semicircle. What will be the electric field intensity at the centre of curvature of the semicircle thus formed?
View SolutionA positive charge Q is uniformly distributed along the length L of a rod. It is bent in the shape of a square. Calculate electric field intensity at the centre of the square.
View Solution
Knowledge Check
A thin rod of length L is bent to form a semi circle. The mass of the rod is M. What will be the gravitational potential at the centre of the circle?
A−GMLB−GM2πLC−πGM2LD−πGMLA thin of length L is bent to form a semicircle. The mass of rod is M. What will be the gravitational potential at the centre of the circle ?
A−GMLB−GM2πLC−πGM2LD−πGMLAn iron rod of length L and magnetic moment M is bent in the form of a semicircle. Now its magnetic moment will be
AMB2MπCMπDMπ
A wire of length 36 cm is bent in the form of a semicircle. What is the radius of the semicircle?
View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionCharge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to

View SolutionA wire of length l and mass m is bent in the form of a semicircle. The gravitational field intensity at the centre of semicircle is

View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
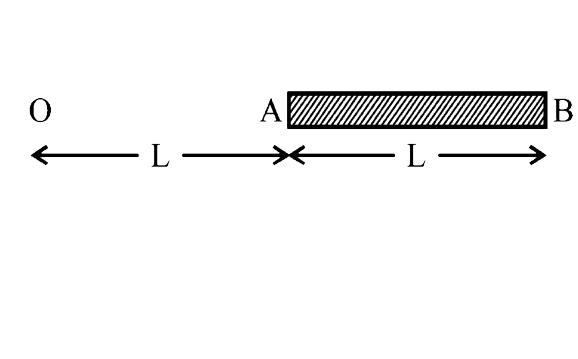
View Solution
