Five identical point charges +Q are placed at the five corners of a regular hexagon of edge length a. One corner is empty. Electric field intensity at the centre of the hexagon is
Zero
Q4πε0d2, towards the empty corner
Q4πε0d2, away from the empty corner
5Q4πε0a2 towards the empty corner
The correct Answer is:B
To find the electric field intensity at the center of a regular hexagon with five identical point charges +Q placed at its corners (with one corner empty), we can follow these steps:
Step 1: Understand the Configuration
We have a regular hexagon with five charges +Q at five of its corners. The sixth corner is empty. The electric field at the center of the hexagon will be influenced by the charges at the corners.
Step 2: Identify the Electric Field Contribution from Each Charge
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant (k=14πϵ0).
Step 3: Determine the Distance from Charges to the Center
In a regular hexagon, the distance from each corner to the center can be calculated. For a hexagon with edge length a, the distance d from the center to any vertex is given by:
d=a√3
Step 4: Calculate the Magnitude of Electric Field from Each Charge
Since all charges are identical and equidistant from the center, the magnitude of the electric field due to each charge at the center is:
Ei=kQd2=kQ(a√3)2=3kQa2
Step 5: Analyze the Direction of Electric Fields
The electric field vectors due to the charges will point away from the charges since they are positive. We have:
- E1 and E4 will cancel each other out.
- E2 and E5 will also cancel each other out.
Step 6: Consider the Remaining Charge
The only charge that does not have a counterpart to cancel it is E3. Therefore, the net electric field at the center will be equal to the electric field due to charge E3.
Step 7: Determine the Direction of the Net Electric Field
The direction of the net electric field will be directed towards the empty corner of the hexagon, as the other charges are pushing away from the center.
Final Result
The magnitude of the electric field at the center of the hexagon is:
E=3kQa2
and the direction is towards the empty corner.
We have a regular hexagon with five charges +Q at five of its corners. The sixth corner is empty. The electric field at the center of the hexagon will be influenced by the charges at the corners.
The electric field E due to a point charge Q at a distance r is given by the formula:
E=kQr2
where k is Coulomb's constant (k=14πϵ0).
In a regular hexagon, the distance from each corner to the center can be calculated. For a hexagon with edge length a, the distance d from the center to any vertex is given by:
d=a√3
Since all charges are identical and equidistant from the center, the magnitude of the electric field due to each charge at the center is:
Ei=kQd2=kQ(a√3)2=3kQa2
The electric field vectors due to the charges will point away from the charges since they are positive. We have:
- E1 and E4 will cancel each other out.
- E2 and E5 will also cancel each other out.
The only charge that does not have a counterpart to cancel it is E3. Therefore, the net electric field at the center will be equal to the electric field due to charge E3.
The direction of the net electric field will be directed towards the empty corner of the hexagon, as the other charges are pushing away from the center.
The magnitude of the electric field at the center of the hexagon is:
E=3kQa2
and the direction is towards the empty corner.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ) )26videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))3videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Numerical Problems )7videos
ELECTRIC CHARGES AND FIELDS
- BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST15videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION14videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Six equal point charges are placed at the corners of a regular hexagon of side 'a'. Calculate electric field intensity at the centre of hexagon ?
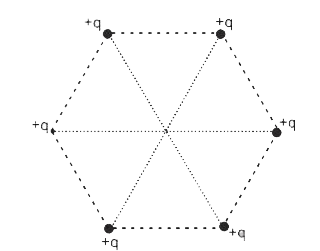 View Solution
View SolutionFour identical point charges, each of charge q, are placed on the vertices of a regular hexagon of side a such that the net electric field at centre of hexagon is zero. If one of the charge is now removed, then the electric field at centre of hexagon is k- 4.60
View Solution
Knowledge Check
- Question 1 - Select One
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq16πε0a2C√2q4πε0a2D5q16πε0a2 - Question 2 - Select One
Five point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
A14πε0qa2Bq2πε0a2C5q4πε0a2D5q2πε0a2 - Question 3 - Select One
Five charges each equal to q are palced at the five corners, A,B,C,D and E of a regular hexagon ABCDEF of side a. Then the electric intensity at he centre O of the hexagon is
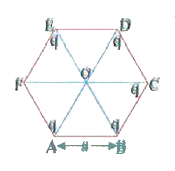 Aq4pe0a2along −−→OFBq4pe0a2 along−−→FOCq4pe03a2 along −−→OFD5q4πe0a2 along −−→OF
Aq4pe0a2along −−→OFBq4pe0a2 along−−→FOCq4pe03a2 along −−→OFD5q4πe0a2 along −−→OF
Three identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
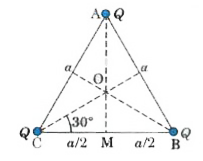 View Solution
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is
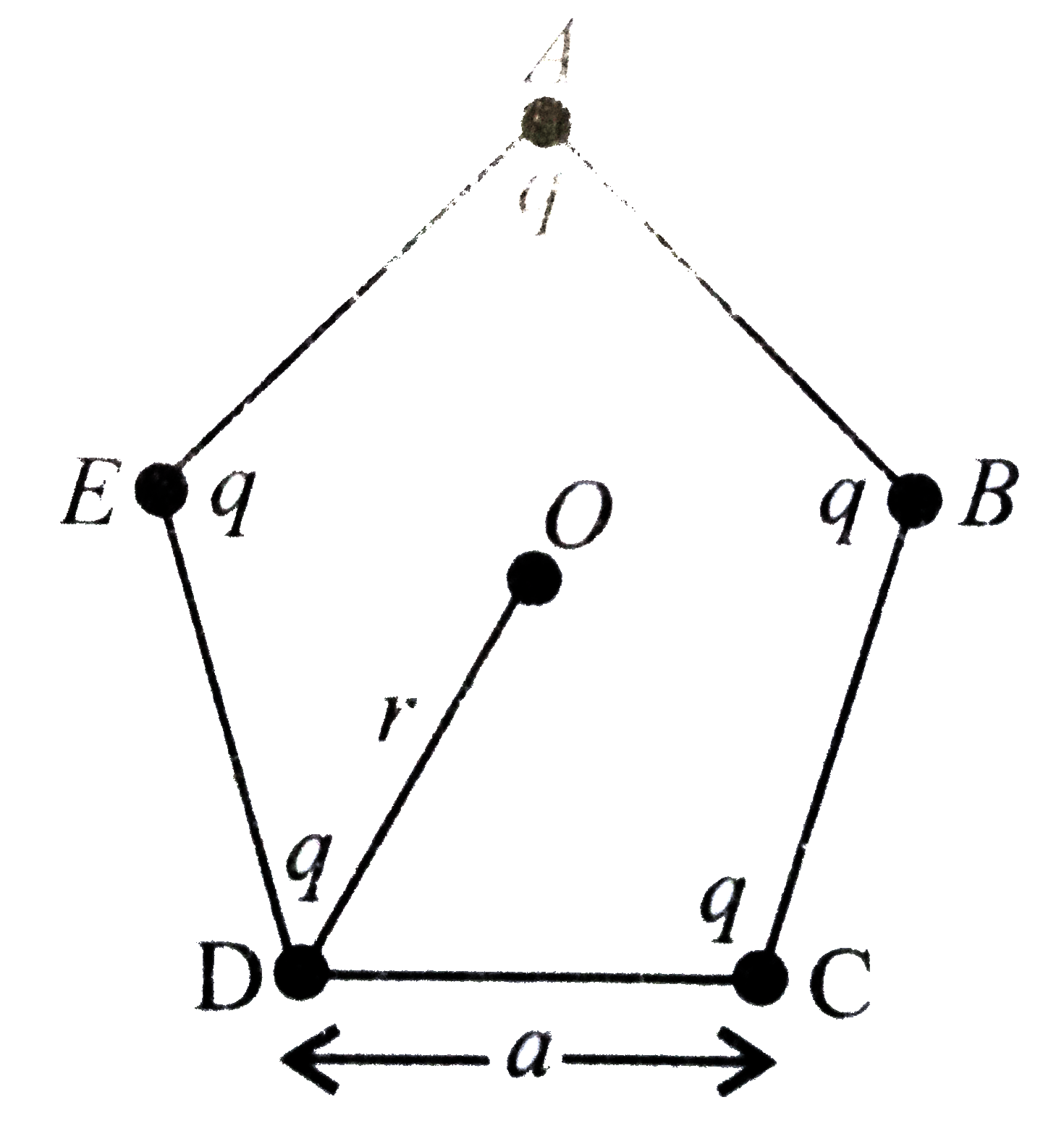 View Solution
View SolutionThere is a pentagon ABCDE, whose centre is O. Five identical charges Q are placed at the corners of pentagon.
(a)What will be the net electric field intensity at the centre of pentagon ?
(b)If charge at corner A is moved to centre O of pentagon, then what will be the net force experienced by it ?
Distance of any vertex of pentagon from its centre is d.
 View Solution
View SolutionSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
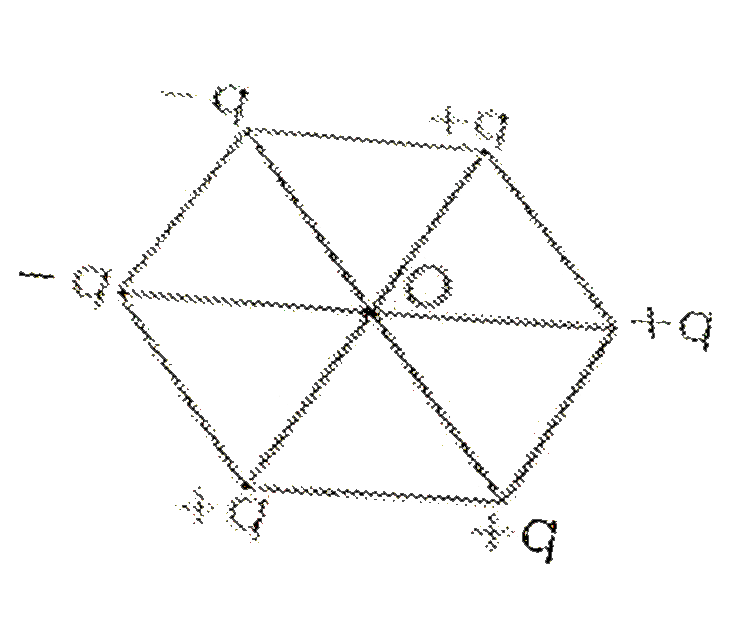
Find the magnitude of electric field at the centre of regular hexagon.View SolutionSix particles each of massm are placed at the corners of a regular hexagon of edge length a. If a point mass m0 is placed at the centre of the hexagon, then the net gravitational force on the point mass is
View Solution

