A uniformly charged solid (non-conducting) sphere of radius R carrying positive charge, has a volume charge density equal to ρ. A tunnel of very small radius is made along the diameter of the sphere. A particle of mass m and charge -q is released from rest near the opening of tunnel described above. Calculate the speed of particle as it passes through the center of the sphere.
Electric potential at a point lying inside a charged solid non-conducting sphere of radius R is given by the following relation:
V+ρ6ε0[3R2−x2] for x≤R
here x is the distance of point from the centre of sphere
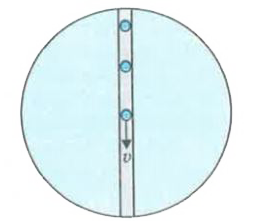
Initial location of particle is at the surface of the sphere.
Let the potential at this point be V1.
Using x = R, in above relation, we have, V1=ρR23ε0
The final location is centre where we need to calculate the speed. Let electric potential at the centre be V2.
Then we can use x = 0 in the formula of electric potential: V2=ρR22ε0
By definition we have:
V2−V1=−Welq⇒Wel=q(V1−V2)
⇒Wel=(−q)(ρR23ε0−ρR22ε0), (note that we have used negative sign of charge in this step).
⇒Wel=ρqR26ε0
For a negatively charged particle
Wel=K2−K1
⇒pqR26ε0=12mv2−0
⇒v=√ρqR23mε0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 1
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 2
Explore 21 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Self energy of conducting sphere of radius .r. carrying charge .Q. is ______
View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
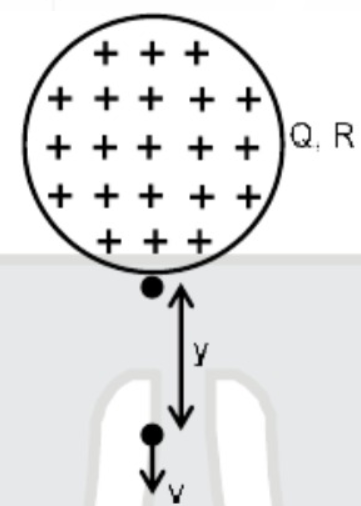
View Solution
Knowledge Check
A uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
 A√2gyB√2kQqymR(R+y)C√2gy+2kQqymR(R+y)D√gy+kQqymR(R+y)
A√2gyB√2kQqymR(R+y)C√2gy+2kQqymR(R+y)D√gy+kQqymR(R+y)A conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
AQ/4BQ/3CQ/2D2Q/3I a uniformly positively charged sphere a very thin tunnel has been made along the diameter as shown in the figure below. A carged particle -q having mass m is released from rest at one end of tunnel. For the situation described, mark out the correct statement (s) : [Neglect gravity]
 ACharged particle will perform SHM about centre of the sphere as mean positionBTime period of the particle is 2π√4πε0mR3qQCParticle will perform oscillation but not SHMDSpeed of the particle while crossing mean positon is √Qq4πε0mR
ACharged particle will perform SHM about centre of the sphere as mean positionBTime period of the particle is 2π√4πε0mR3qQCParticle will perform oscillation but not SHMDSpeed of the particle while crossing mean positon is √Qq4πε0mR
A conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionRepeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View SolutionI a uniformly positively charged sphere a very thin tunnel has been made along the diameter as shown in the figure below. A carged particle -q having mass m is released from rest at one end of tunnel. For the situation described, mark out the correct statement (s) : [Neglect gravity]
View SolutionThere is a solid non-conducting sphere of radius R. Sphere is uniformly charged over the volume. Electric field due to this where in observed.
View SolutionCalculate amount of charge flow, when a conducting sphere of radius R and carrying a charge Q, is joined to an uncharged conducting sphere of radius 2R.
View Solution
