I a uniformly positively charged sphere a very thin tunnel has been made along the diameter as shown in the figure below. A carged particle -q having mass m is released from rest at one end of tunnel. For the situation described, mark out the correct statement (s) : [Neglect gravity]
Charged particle will perform SHM about centre of the sphere as mean position
Time period of the particle is 2π√4πε0mR3qQ
Particle will perform oscillation but not SHM
Speed of the particle while crossing mean positon is √Qq4πε0mR
The correct Answer is:A, B, D
To solve the problem, we need to analyze the motion of a charged particle placed in a uniformly charged sphere with a tunnel along its diameter. We will determine whether the charged particle performs simple harmonic motion (SHM) and derive the relevant expressions.
1. Understanding the System:
- We have a uniformly positively charged sphere.
- A charged particle of charge −q (negative charge) is placed at one end of a tunnel that runs through the diameter of the sphere.
- The gravitational force is neglected.
2. Electric Field Inside the Sphere:
- According to Gauss's law, the electric field E inside a uniformly charged sphere at a distance r from the center is given by:
E=Q4πϵ0R3r
where Q is the total charge of the sphere, R is the radius of the sphere, and r is the distance from the center.
3. Force on the Charged Particle:
- The force F acting on the particle due to the electric field is:
F=−qE=−q(Q4πϵ0R3r)
- This indicates that the force is directed towards the center of the sphere when the particle is displaced from the center, which is a characteristic of SHM.
4. Condition for SHM:
- For SHM, the force must be proportional to the displacement from the mean position, i.e., F∝−r.
- From the force expression, we see that:
F=−qQ4πϵ0R3r
- This confirms that the motion is indeed SHM with k=qQ4πϵ0R3.
5. Finding the Time Period of SHM:
- The time period T of SHM is given by:
T=2π√mk=2π√m⋅4πϵ0R3qQ
6. Speed at Mean Position:
- The speed v of the particle as it crosses the mean position can be derived using the relationship between angular frequency ω and speed:
v=ωr
- Here, ω=√km=√qQ4πϵ0mR3, thus:
v=√qQ4πϵ0mR
Conclusion:
From the analysis, we conclude that:
- The charged particle will perform SHM about the center of the sphere.
- The time period of the oscillation is given by T=2π√4πϵ0mR3qQ.
- The speed of the particle as it crosses the mean position is given by v=√qQ4πϵ0mR.
- We have a uniformly positively charged sphere.
- A charged particle of charge −q (negative charge) is placed at one end of a tunnel that runs through the diameter of the sphere.
- The gravitational force is neglected.
- According to Gauss's law, the electric field E inside a uniformly charged sphere at a distance r from the center is given by:
E=Q4πϵ0R3r
where Q is the total charge of the sphere, R is the radius of the sphere, and r is the distance from the center.
- The force F acting on the particle due to the electric field is:
F=−qE=−q(Q4πϵ0R3r)
- This indicates that the force is directed towards the center of the sphere when the particle is displaced from the center, which is a characteristic of SHM.
- For SHM, the force must be proportional to the displacement from the mean position, i.e., F∝−r.
- From the force expression, we see that:
F=−qQ4πϵ0R3r
- This confirms that the motion is indeed SHM with k=qQ4πϵ0R3.
- The time period T of SHM is given by:
T=2π√mk=2π√m⋅4πϵ0R3qQ
- The speed v of the particle as it crosses the mean position can be derived using the relationship between angular frequency ω and speed:
v=ωr
- Here, ω=√km=√qQ4πϵ0mR3, thus:
v=√qQ4πϵ0mR
From the analysis, we conclude that:
- The charged particle will perform SHM about the center of the sphere.
- The time period of the oscillation is given by T=2π√4πϵ0mR3qQ.
- The speed of the particle as it crosses the mean position is given by v=√qQ4πϵ0mR.
Similar Questions
A particle of mass ma and charge q has been projected from ground as shown in fig. Mark the correct statement(s) (xy) plane is vertical.

View SolutionA uniformly charged sphere of charge Q and radius R is placed at some height from ground surface and sphere is fixed. Now a charged particle of mass m and charge q is released form rest just below to sphere what will be speed of particle after travelling Y-direction
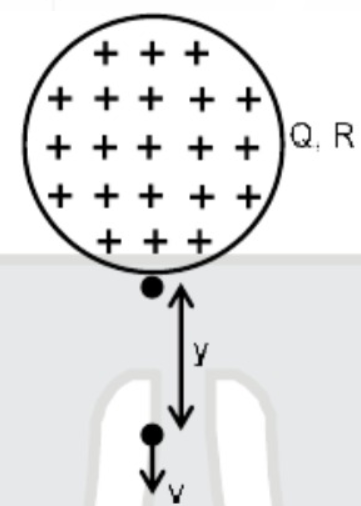
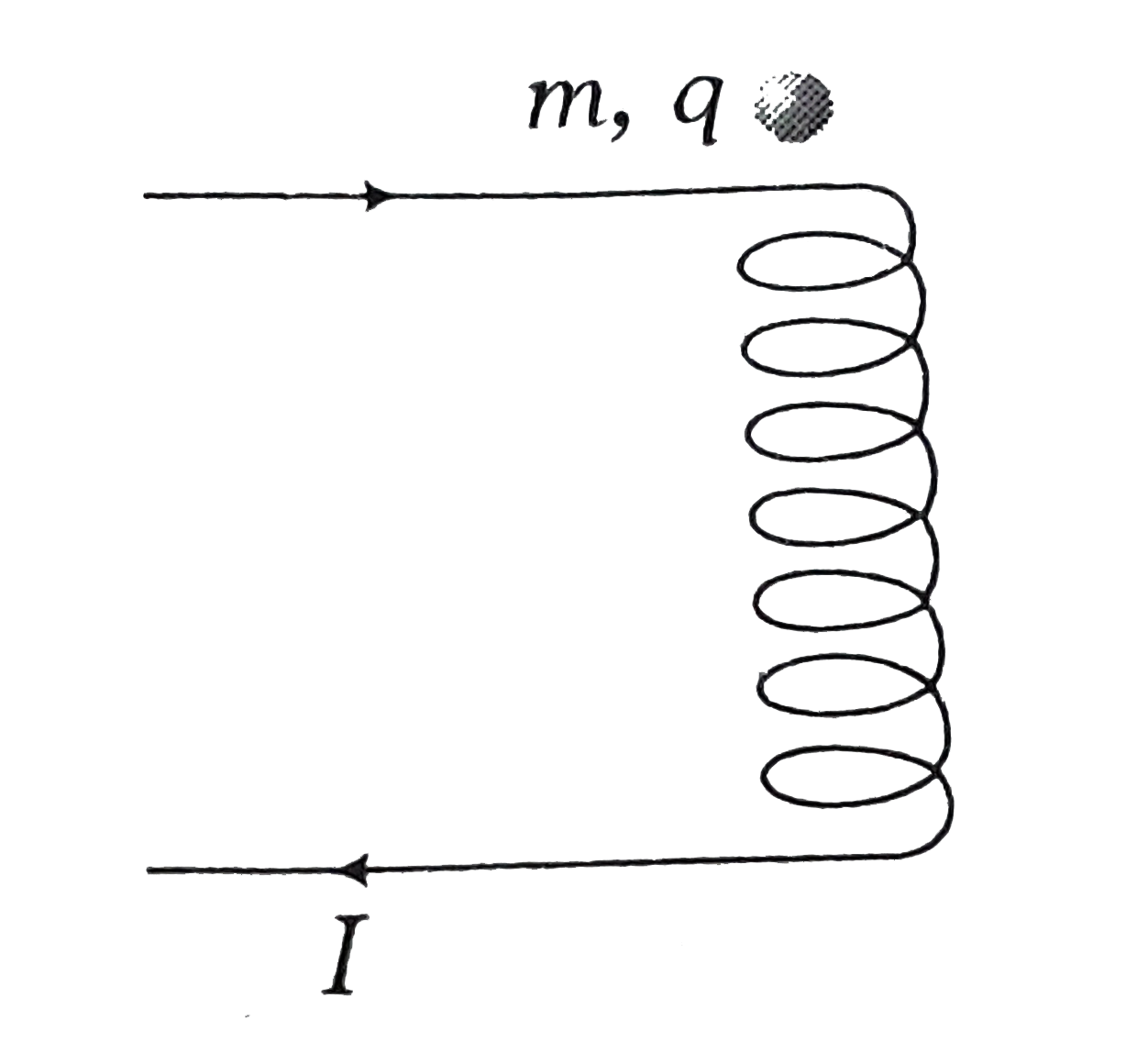
View SolutionA long solenoid carrying a current I is placed with its axis vertical as shown in the figure. A particle of mass m and charge q is released from the top of the solenoid. Its acceleration is (g being acceleration due to gravity)
View SolutionSuppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of the earth is uniformly distributed over its volume. Then, which of the following statements are not correct?
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphere
View SolutionA light rigid rod of length l is hinged at one end and it is free to rotate in a vertical plane. A particle of mass m is attached to another end of the rod. The particle is released from rest at its highest point. Select the correct statement out of the following
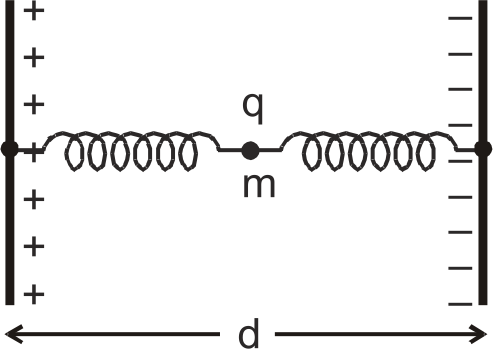
View SolutionTwo large non conducting plates having surface charge densities +σ and −σ respectively, are fixed d distnce apart. A small test charge q of mass m is attached to two non conducting springs each of spring constant k as shown in the figure. The sum of lengths of both springs in underformed state is d. The charge q is released from rest with both the springs nondeformed. then charge q will (neglect gravity)
View SolutionStatement I: In free space a uniform spherical planet of mass M has a smooth narrow tunnel along its diameter. This planet and another superdense small particle of mass M start approaching towards each other from rest under action of their gravitational forces. When the particle passes through the centre of the planet, sum of kinetic energies of both the bodies is maximum.
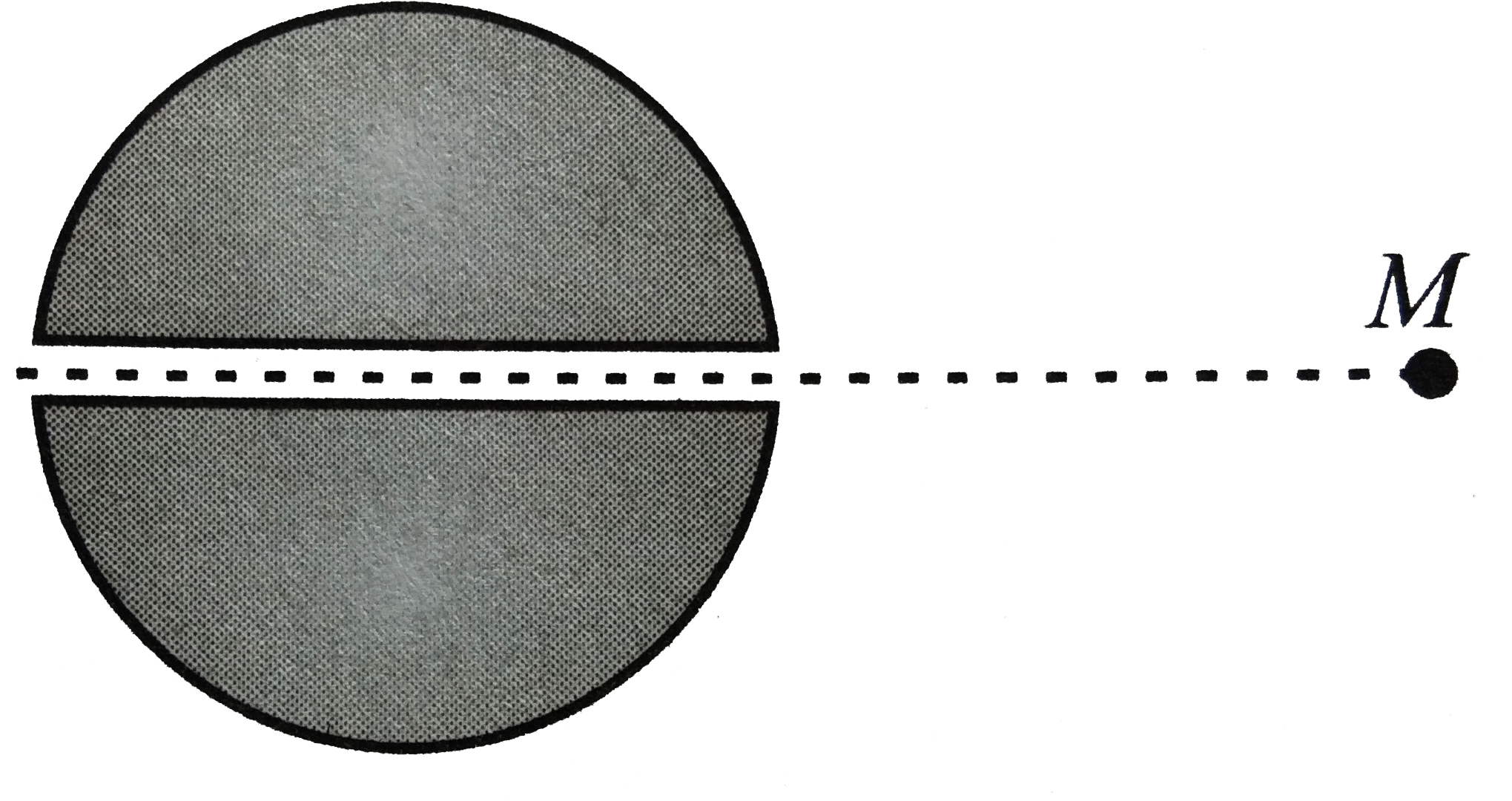
Statement II: When the resultant of all forces acting on a particle or a particle like object (initially at rest) is constant in direction, the kinetic energy of the particle keeps on increasing.
View SolutionTwo large insulating plates having surface charge densities +σ and −σ are fixed some distance apart in a gravity -free region and two ideal insulating springs of force constant k are connected to the plates as shown in the figure. A particle of charge q and mass m which is attached to the junction of the spring is released from rest, then the partice will cross its equilibrium position with a speed
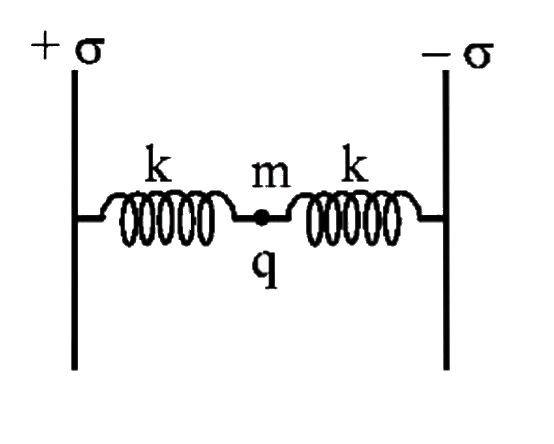
View SolutionA circular loop of radius R is bent along a diameter and given a shape as shown in figure. One of 30,A the se micircles (KNM) lies in the xz-plane and the other one (KLM) in the yz-plane with their centres at origin. Current I is flowing through each of the semicircles as shown in figure.
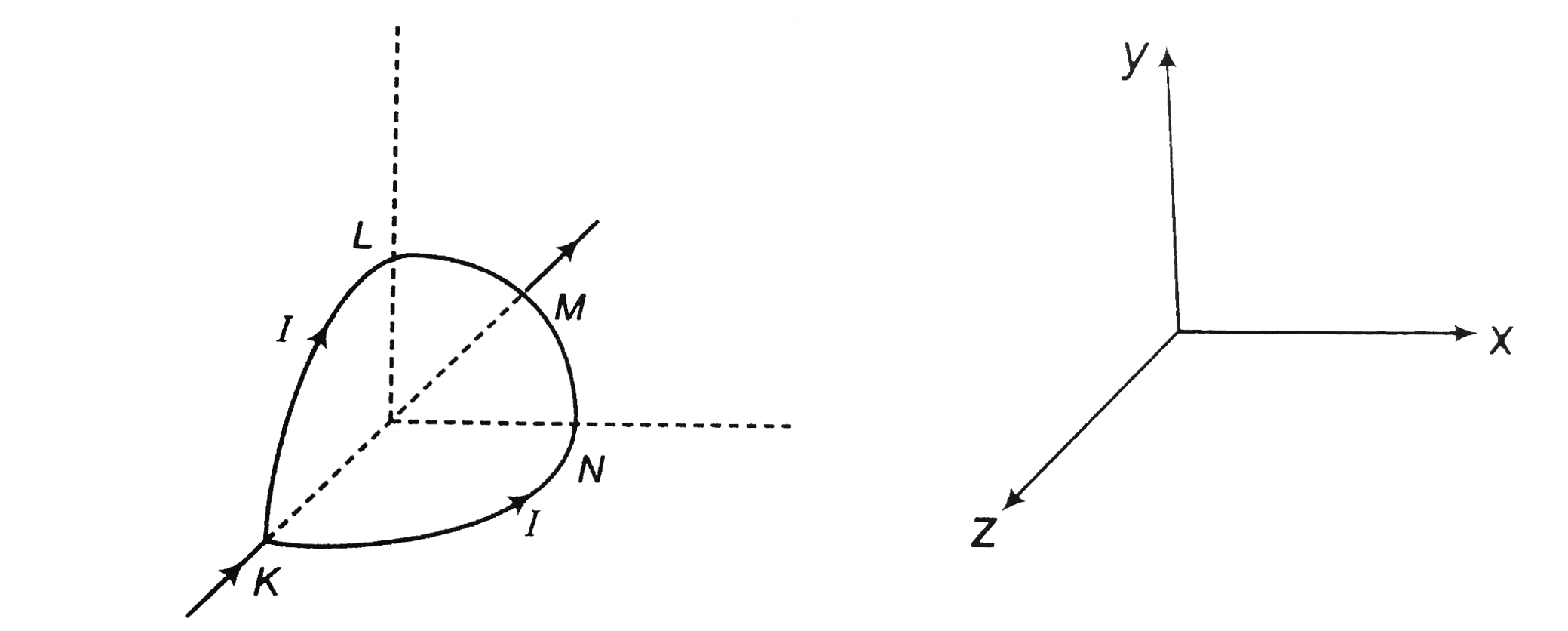
(a) A particle of charge q is released at the origin with a velocity v=−v0ˆi. Find the instantaneous force F on the particle. Assume that space is gravity free.
(b) If an external uniform magnetic field B0ˆj is applied, determine the force F1 and F2 on the semicircles KLM and KNM due to the field and the net force F on the loop.
View Solution
