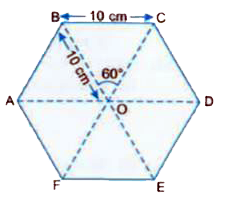
A regular hexagon of side 10 cm has a charge $5 μ C$ at each of its vertices. Calculate the potential at the center of the hexagon.

Video Solution

Text Solution

Verified by Experts

A we know that electric potential is a scalar quantity and due to a system of charges electric potential is the algebraic sum of the electric potential due to the individual charges. As a regular hexagon is given here, the distance of the centre from each corner is same as the side length of the hexagon.
Thus, the electric potential at point O due to all the charges can be calculated as:
$V = 6 \times \frac{1}{4 π ε_{0}} \frac{q}{r}$
$= \frac{6 \times 9 \times 10^{9} \times 5 \times 10^{- 6}}{0.1}$
$= 2.7 \times 10^{6}$ volt

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A hexagon of side 8 cm has a charge $4 μ C$ at each of its vertices. The potential at the centre of the hexagon is
A $2.7 \times 10^{6} V$
B $7.2 \times 10^{11} V$
C $2.5 \times 10^{12} V$
D $3.4 \times 10^{4} V$
Question 2 - Select One
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A $0$
B $\frac{1}{4 π \in_{0}} . \frac{q}{a^{2}}$
C $\frac{1}{4 π \in_{0}} . \frac{6 q}{a^{2}}$
D $\frac{1}{4 π \in_{0}} . \frac{6 q^{2}}{a^{2}}$
Question 3 - Select One
A wire shaped to a regular hexagon of side x carries a current I ampere. Calculate the strength of the magnetic field at the centre of the hexagon.
A $\frac{\sqrt{3} μ_{0} I}{π x}$
B $\frac{3 μ_{0} I}{π x}$
C $\frac{μ_{0} I}{3 π x}$
D $\frac{μ_{0} I}{\sqrt{3} π x}$

MODERN PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE -NCERT FILE Solved (Textbook Exercise)

Home
Ask Doubt
Profile