Question

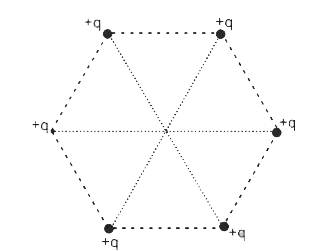
A regular hexagon of side $a$ has a charge Q at each vertex. Potential at the centres of hexagon is (k= $\left(\frac{1}{4}\pi {\epsilon }_0\right)$)

Options

A. Zero
B. `kQ/a`
C. `12(kQ)/a `
D. `6(kQ)/a `

Answer

D

Explanation

To find the electric potential at the center of a regular hexagon with a charge $$Q$$ at each vertex, we can follow these steps:

Step 1: Understand the Geometry
A regular hexagon has six vertices, and each vertex has a charge \( Q \). The distance from each vertex to the center of the hexagon is the same due to its symmetry. Let's denote this distance as \( r \).

Step 2: Calculate the Distance from Vertex to Center
For a regular hexagon with side length \( a \), the distance from any vertex to the center can be calculated using the formula:
\( r = \frac{a}{\sqrt{3}} \quad \text{(for a regular hexagon)} \)
However, for the potential calculation, we can just use the side length \( a \) directly since the potential depends on the distance from the charge to the point where the potential is being calculated.

Step 3: Write the Formula for Electric Potential
The electric potential \( V \) due to a single point charge \( Q \) at a distance \( r \) is given by:
\( V = \frac{kQ}{r} \)
where \( k = \frac{1}{4\pi\epsilon_0} \).

Step 4: Calculate the Total Potential at the Center
Since the potential is a scalar quantity, we can simply add the potentials due to each charge at the center. There are six charges, so the total potential \( V_{total} \) at the center is:
\( V_{total} = 6 \cdot \frac{kQ}{r} \)
Substituting \( r = a \):
\( V_{total} = 6 \cdot \frac{kQ}{a} \)

Step 5: Final Expression for Potential
Thus, the potential at the center of the hexagon is:
\( V = \frac{6kQ}{a} \)

Conclusion
The potential at the center of the hexagon with a charge \( Q \) at each vertex is:
\( V = \frac{6kQ}{a} \)