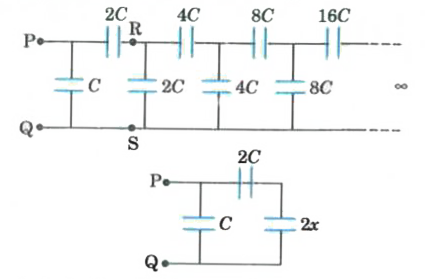
Consider the following network of capacitors extended up to infinity and find the equivalent capacitance between P and Q.
Video Solution
Text Solution
We can understand that the equivalent capacitance between P and Q must be the same as net capacitance between R and S due to the repeating nature of this network.
Let x be the net capacitance of this network between points P and Q then it must be same between R and S. We can understand it with the help of the following diagram.
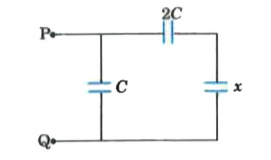
x=C+2Cx2C+x
⇒x=2C2+Cx+2Cx2C+x
⇒2Cx+x2=2C2+Cx+2Cx⇒x2−Cx−2C2=0
x=C±√C2+8C22⇒x=C±3C2⇒x=2C&−C
2C is the correct answer.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Very Short Answer Questions)56videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Additional Questions)10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Exemplar Problems) (Short Answer Type Questions)5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the equivalent capacitance between A and B
 A5μFB4μFC3μFD2μF
A5μFB4μFC3μFD2μF - Question 2 - Select One
The equivalent capacitance between P and Q is.
 .A10μFB20μFC5μFD15μF
.A10μFB20μFC5μFD15μF
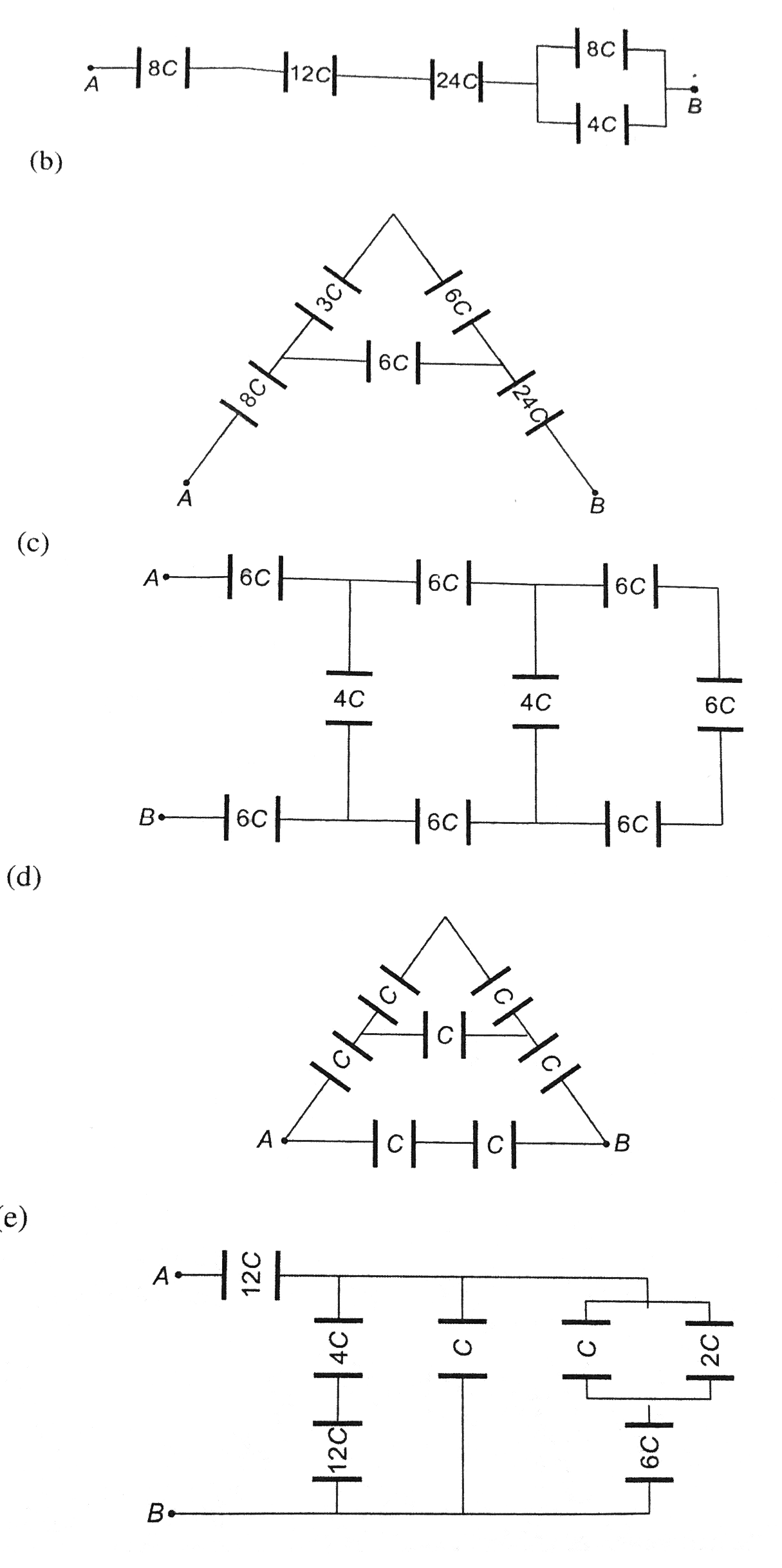
Find the equivalent capacitance between A and B.
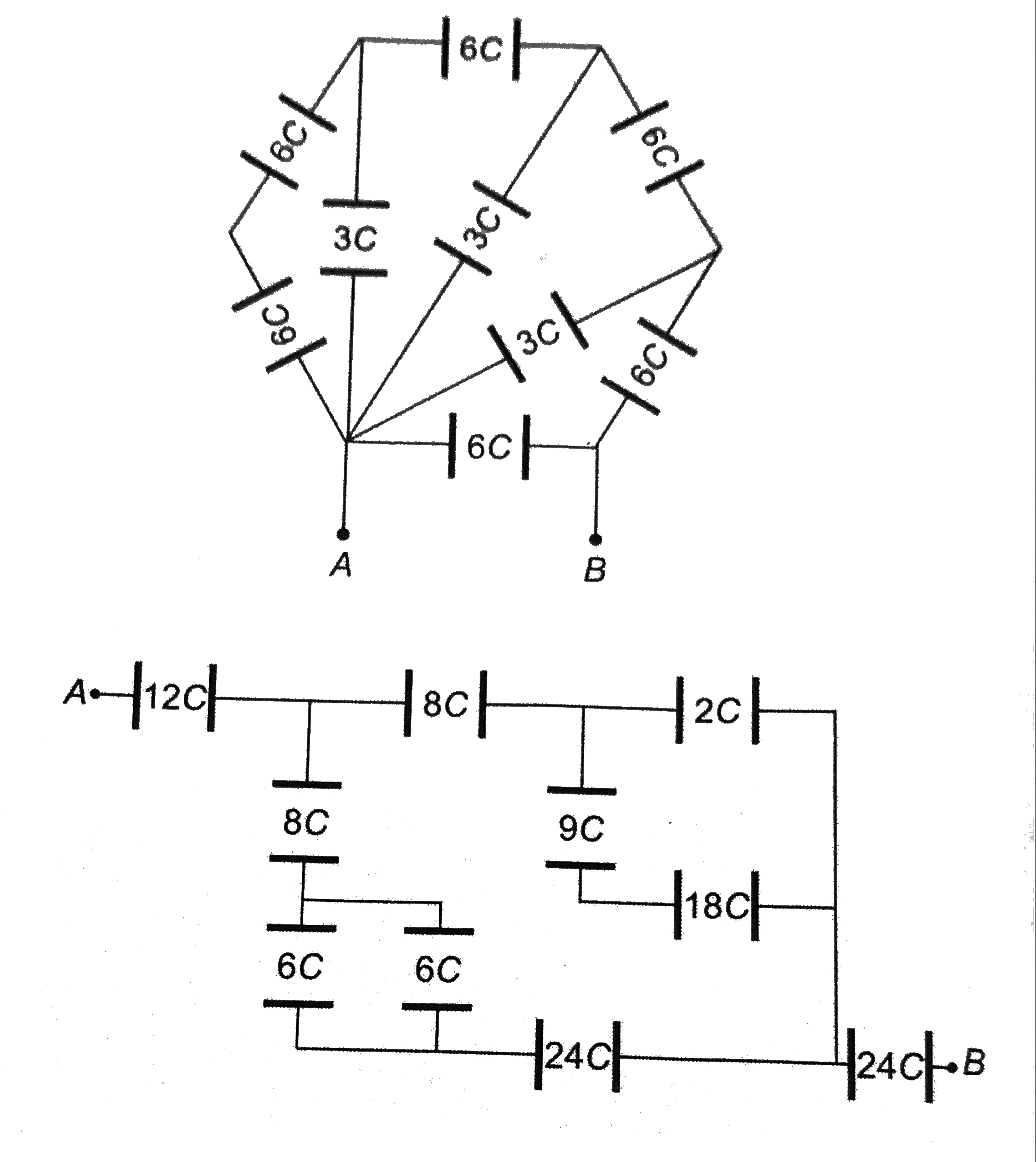 View Solution
View SolutionFind the equivalent capacitance between A and B.
 View Solution
View SolutionFind the equivalent capacitance between A and B.

 View Solution
View SolutionFind the equivalent capacitance between A and B.
 View Solution
View SolutionFind the equivalent capacitance between A and B.
 View Solution
View SolutionFind the equivalent capacitance between A&B
View Solution