Assertion: If electric potential remains constant along a path in electric field, then the electric field must be zero.
Reason: The negative of an electric potential gradient in a direction is equal to the component of electric field in that direction.
If both assertion and reason are correct and reason is a correct explanation of the assertion.
If both assertion and reason are correct but reason is not the correct explanation of assertion.
If assertion is correct but reason is incorrect.
If assertion is incorrect but reason is correct.
The correct Answer is:d
To solve the given question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
- The assertion states that "If electric potential remains constant along a path in an electric field, then the electric field must be zero."
- If the electric potential (V) is constant along a path, it implies that there is no change in potential energy as we move along that path.
2. Understanding the Reason:
- The reason states that "The negative of an electric potential gradient in a direction is equal to the component of electric field in that direction."
- Mathematically, this can be expressed as:
E=−dVdx
- This means that the electric field (E) is related to how the electric potential (V) changes with position (x). If the potential is constant, then the gradient (or derivative) is zero, leading to zero electric field in that direction.
3. Analyzing the Assertion:
- The assertion is incorrect because even if the electric potential is constant along a path, it does not necessarily mean that the electric field is zero. The electric field can still exist but may be perpendicular to the path taken.
- For example, in the case of an equipotential surface, the electric field lines are perpendicular to the surface, meaning the potential is constant along the surface, but the electric field is not zero.
4. Conclusion:
- The assertion is incorrect because the electric field can be non-zero even when the potential is constant along a path.
- The reason is correct because it accurately describes the relationship between electric field and potential gradient.
5. Final Answer:
- The assertion is incorrect, and the reason is correct. Therefore, the correct choice is that the assertion is false, and the reason is true.
- The assertion states that "If electric potential remains constant along a path in an electric field, then the electric field must be zero."
- If the electric potential (V) is constant along a path, it implies that there is no change in potential energy as we move along that path.
- The reason states that "The negative of an electric potential gradient in a direction is equal to the component of electric field in that direction."
- Mathematically, this can be expressed as:
E=−dVdx
- This means that the electric field (E) is related to how the electric potential (V) changes with position (x). If the potential is constant, then the gradient (or derivative) is zero, leading to zero electric field in that direction.
- The assertion is incorrect because even if the electric potential is constant along a path, it does not necessarily mean that the electric field is zero. The electric field can still exist but may be perpendicular to the path taken.
- For example, in the case of an equipotential surface, the electric field lines are perpendicular to the surface, meaning the potential is constant along the surface, but the electric field is not zero.
- The assertion is incorrect because the electric field can be non-zero even when the potential is constant along a path.
- The reason is correct because it accurately describes the relationship between electric field and potential gradient.
- The assertion is incorrect, and the reason is correct. Therefore, the correct choice is that the assertion is false, and the reason is true.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MATCHING TYPE QUESTIONS)3videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MATRIX TYPE QUESTIONS)1videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)17videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
For an electric dipole potential & electric field
Acan have same magnitude for a point at a distance less than 2 meterBcan have same magnitude fo a point at distacnes greater than 2 meterCcan never be equalDcan never be predicted - Question 2 - Select One
Assertion : Electric potential of earth is taken zero.
Reason : No electric field exists on earth surface.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false. - Question 3 - Select One
In a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
AAlso constantBPositiveCNegativeDZero
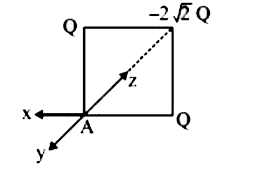
For the given figure the direction of electric field at A will be
 View Solution
View SolutionElectric intensity is directed along the direction at which electric potential
View SolutionStatement I: If electric potential in certain region is constant, then the electric field must be zero in this region.
Statement II: →E=−dVdrˆv.View SolutionWhen a negative charge moves in a direction opposite to the direction of an electric field,
View SolutionThe neagative gradient of potential at any point in electric field is
View Solution

