Show that the electric field intensity at a point can be given as negative of potential gradient.
To show that the electric field intensity at a point can be given as the negative of the potential gradient, we can follow these steps:
Step 1: Define Electric Potential
Electric potential (V) at a point in an electric field is defined as the work done (W) in bringing a unit positive charge from infinity to that point against the electric field. Mathematically, it can be expressed as:
V=−∫P∞→E⋅d→r
where →E is the electric field intensity and d→r is the infinitesimal displacement vector.
Step 2: Consider a Test Charge
Let's consider a test charge Q0 that is moved from a point at infinity to a point P in the electric field created by a charge Q. The work done by the external agent in moving the charge is equal to the change in potential energy.
Step 3: Work Done by Electric Field
When the charge Q0 is moved a small distance dR in the direction of the electric field, the work done by the electric field on the charge is:
dW=→E⋅d→r
Since the electric field does work on the charge, the work done against the electric field is negative:
dW=−→E⋅d→r
Step 4: Relate Work Done to Potential
The potential difference dV between two points can be expressed as the work done per unit charge:
dV=dWQ0
Substituting our expression for dW:
dV=−→E⋅d→rQ0
Step 5: Express Electric Field in Terms of Potential
Now, we can rearrange the equation to find the electric field:
→E=−dVdR
This indicates that the electric field intensity →E at point P is the negative gradient of the electric potential V.
Step 6: Conclusion
Thus, we have shown that the electric field intensity at any point can be expressed as:
→E=−∇V
This means that the electric field points in the direction of decreasing potential, confirming that the electric field intensity is the negative of the potential gradient.
Electric potential (V) at a point in an electric field is defined as the work done (W) in bringing a unit positive charge from infinity to that point against the electric field. Mathematically, it can be expressed as:
V=−∫P∞→E⋅d→r
where →E is the electric field intensity and d→r is the infinitesimal displacement vector.
Let's consider a test charge Q0 that is moved from a point at infinity to a point P in the electric field created by a charge Q. The work done by the external agent in moving the charge is equal to the change in potential energy.
When the charge Q0 is moved a small distance dR in the direction of the electric field, the work done by the electric field on the charge is:
dW=→E⋅d→r
Since the electric field does work on the charge, the work done against the electric field is negative:
dW=−→E⋅d→r
The potential difference dV between two points can be expressed as the work done per unit charge:
dV=dWQ0
Substituting our expression for dW:
dV=−→E⋅d→rQ0
Now, we can rearrange the equation to find the electric field:
→E=−dVdR
This indicates that the electric field intensity →E at point P is the negative gradient of the electric potential V.
Thus, we have shown that the electric field intensity at any point can be expressed as:
→E=−∇V
This means that the electric field points in the direction of decreasing potential, confirming that the electric field intensity is the negative of the potential gradient.
Topper's Solved these Questions
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - SHORT ANSWER QUESTIONS (3 MARKS )
23 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - LONG ANSWER QUESTIONS
6 Videos
- ELECTROSTATICS AND CURRENT ELECTRICITY BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTROSTATICS AND CURRENT ELECTRICITY EXERCISE - NUMERICALS
49 Videos
- ELECTRONIC DEVICES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ELECTRONIC DEVICES EXERCISE - NUMERICALS
7 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
Knowledge Check
Electric field intensity at a point varies as r−3 for
AA point chargeBAn electric dipoleCA plane infinite sheet of chargeDA line charge of infinite lengthElectric lines of force about negative point charge are
ACircular, anticlockwiseBCircular, clockwiseCRadial, inwardsDRadial , outwardsGravitational force is a conservation and medium independent force. Its nature is attractive. Gravitational field intensity and gravitational potential gives information about gravitational fied in vector and scaler form respectively. Actually gravitational fied intensity is equal to the negative of the negative of teh potential gradient. potential energy is defined for only conservation force. it is also equal to the total energy in escaping condition. gravitational potential is either negative or zero but can never be positive due to attractive nature of gravitational force.
Gravitational potential versus distance r graph is represented in figure. The magnitude of gravitational field intensity is equal to
 A8 Newton /kgB4 Newton /kgC6 Newton/kgD2 Newton/kg
A8 Newton /kgB4 Newton /kgC6 Newton/kgD2 Newton/kg
Gravitational force is a conservation and medium independent force. Its nature is attractive. Gravitational field intensity and gravitational potential gives information about gravitational fied in vector and scaler form respectively. Actually gravitational fied intensity is equal to the negative of the negative of teh potential gradient. potential energy is defined for only conservation force. it is also equal to the total energy in escaping condition. gravitational potential is either negative or zero but can never be positive due to attractive nature of gravitational force.
A person brings a mass of 1kg from infinity to a point A. Initially the mass was at rest but it moves with a speed of 2m/s as it reaches A. The work done by the person on a mass is −3J. The potential of A is:
View SolutionGravitational force is a conservation and medium independent force. Its nature is attractive. Gravitational field intensity and gravitational potential gives information about gravitational fied in vector and scaler form respectively. Actually gravitational fied intensity is equal to the negative of the negative of teh potential gradient. potential energy is defined for only conservation force. it is also equal to the total energy in escaping condition. gravitational potential is either negative or zero but can never be positive due to attractive nature of gravitational force.
The gravitational potential inside a hollow sphere (mass M, radius R) at a distance r from the centre is:
View SolutionElectric field intensity at a point a hollow charged spherical conductor
View SolutionAssertion: If electric potential remains constant along a path in electric field, then the electric field must be zero.
Reason: The negative of an electric potential gradient in a direction is equal to the component of electric field in that direction.
View SolutionFigure shows the variation of electric field intensity E versus distance x. What is the potential difference between the point at x = 2 m and at x = 6 m from O?
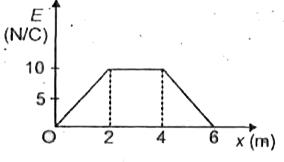
View Solution
