If there is no torsion in the suspension thread, then the time period of a magnet executing oscillation is:
T=12π√MB1
T=12π√1MB
T=2π√IMB
T=2π√MBI
The correct Answer is:C
To solve the problem of finding the time period of a magnet executing oscillation when there is no torsion in the suspension thread, we can follow these steps:
Step 1: Understand the Forces Acting on the Magnet
When the magnet is displaced from its equilibrium position, it experiences a restoring torque due to gravity. The torque (τ) can be expressed as:
τ=mgsinθ
where m is the mass of the magnet, g is the acceleration due to gravity, and θ is the angle of displacement from the vertical.
Step 2: Relate Torque to Angular Acceleration
According to Newton's second law for rotation, the torque is also related to angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the magnet about the pivot point.
Step 3: Set Up the Equation
From the two expressions for torque, we can equate them:
mgsinθ=Iα
Substituting α with the angular displacement, we have:
α=d2θdt2
Thus, we can write:
mgsinθ=Id2θdt2
Step 4: Approximate for Small Angles
For small angles, we can use the approximation sinθ≈θ:
mgθ≈Id2θdt2
Step 5: Rearranging the Equation
Rearranging gives us:
d2θdt2+mgIθ=0
This is the standard form of the simple harmonic motion equation, where:
ω2=mgI
Step 6: Find the Time Period
The time period T of a simple harmonic oscillator is given by:
T=2π√Img
Step 7: Final Expression for Time Period
Thus, the time period of the magnet executing oscillation is:
T=2π√Img
Conclusion
The final answer for the time period of a magnet executing oscillation when there is no torsion in the suspension thread is:
T=2π√Img
When the magnet is displaced from its equilibrium position, it experiences a restoring torque due to gravity. The torque (τ) can be expressed as:
τ=mgsinθ
where m is the mass of the magnet, g is the acceleration due to gravity, and θ is the angle of displacement from the vertical.
According to Newton's second law for rotation, the torque is also related to angular acceleration (α) by:
τ=Iα
where I is the moment of inertia of the magnet about the pivot point.
From the two expressions for torque, we can equate them:
mgsinθ=Iα
Substituting α with the angular displacement, we have:
α=d2θdt2
Thus, we can write:
mgsinθ=Id2θdt2
For small angles, we can use the approximation sinθ≈θ:
mgθ≈Id2θdt2
Rearranging gives us:
d2θdt2+mgIθ=0
This is the standard form of the simple harmonic motion equation, where:
ω2=mgI
The time period T of a simple harmonic oscillator is given by:
T=2π√Img
Thus, the time period of the magnet executing oscillation is:
T=2π√Img
The final answer for the time period of a magnet executing oscillation when there is no torsion in the suspension thread is:
T=2π√Img
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION)JEE ADVANCED FOR IIT ENTRANCE)
2 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((C ) MULTIPLE CHOICE QUESTION)
10 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTION ((B) MULTIPLE CHOICE QUESTION)AIPMT/NEET AND OTHER STATE FOR MEDICAL ENTRANCE)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Chapter Practice Test
9 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - CHAPTER PRACTICE TEST
13 Videos
Similar Questions
A circular disc of mass 12 kg is suspended by a wire attached to its centre. The wire is twisted by rotating the disc and then released, so that the time period of torsional oscillation is 2 s. If the radius of the disc is 10 cm, then calculate the torsional spring constant of the wire.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View Solution
Knowledge Check
A thin magnetic iron rod of length 30 cm is suspended in a uniform magnetic field. Its time period of oscillation is 4s. It is broken into three equal parts. The time period in second of oscillation of one part. When suspended in the same magnetic field, is
A1√3B2√3C√3D4√3Time period of oscillation of a magnetic needle is
AT=√TMBBT=2π√IMBCT=2π√MBIDT=π√MBIA magnet of magnetic moment M oscillates in magnetic field B with time period 2 sec. If now the magnet is cut into two half pieces parallel to the axis, then what is new time period is only one part oscillate in field?
A2 sB2√2sC1√2sD2.4s
Find time period of oscillation of the system.

View SolutionA bar magnet suspended freely has period of oscillation of 2s. Now, the bar magnet is broken into equal halves and one-half is suspended to oscillate freely in the same magnetic field. Find the time period of oscillation of this half of the magnet.
View SolutionThe length, breadth and mass of two bar magnets are same but their magnetic moments are 3M and 2M respectively. These are joined pole to pole and are suspended by a string. When oscillated in a magnetic field of strength B, the time period obtained is 5s. If the poles of either of the magnets are reverse then the time period of the combination in the same magnetic field will be –
View SolutionA uniform meter stickis suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
View SolutionA bar magnet oscillates in a region of uniform magnetic field with time period T . Now , a piece of wood identical in all respects in terms of mass and length is joined with bar magnet as shown . The new time period of oscillation is
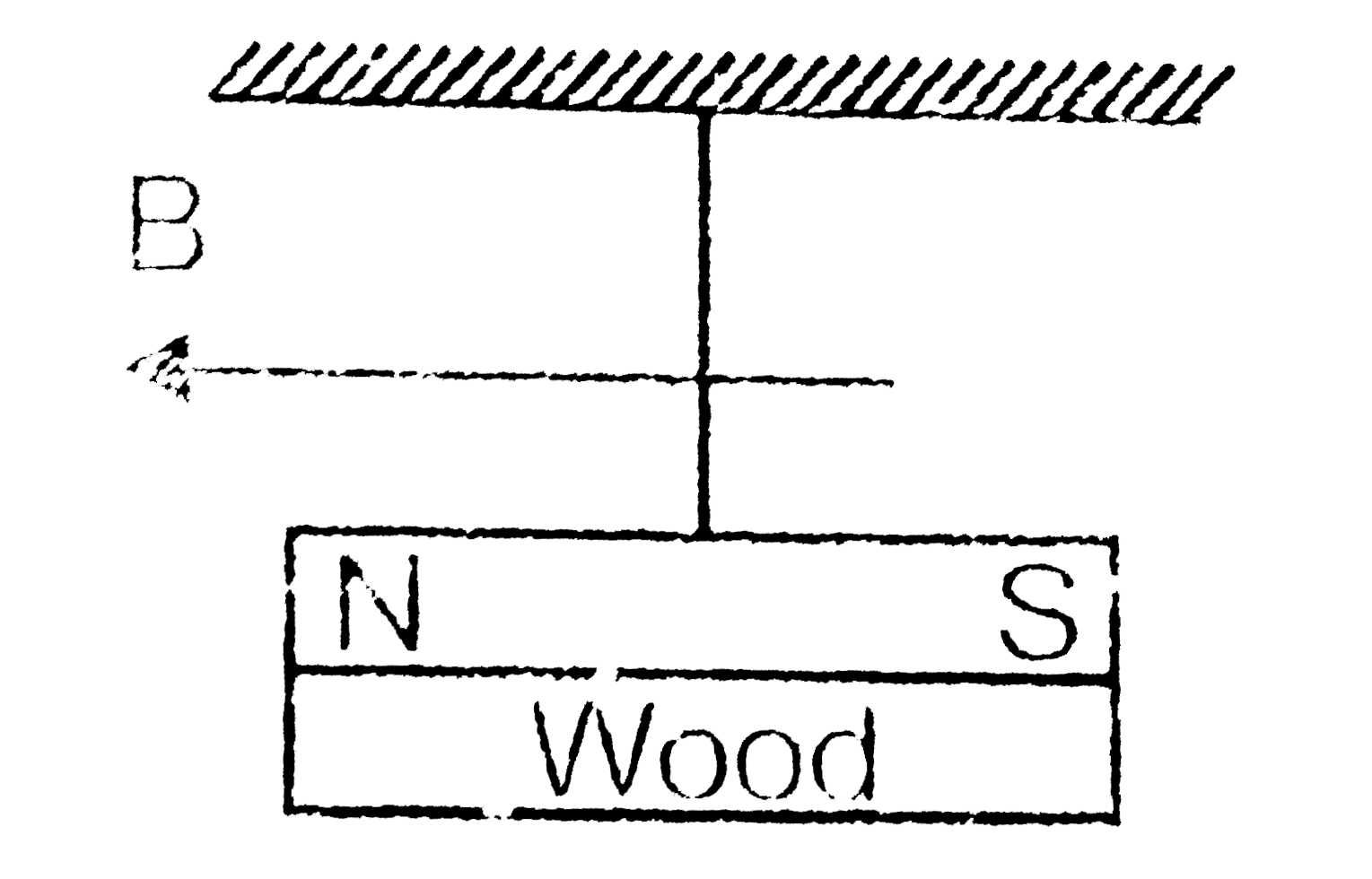
View Solution
