There are two long parallel wire carrying current I in opposite directions are separated by a distance 3a. There is a square loop of size a×a kept in between. The square loop contains a capacitor of capacitance C, as shown in figure. If current in wires changes with time as I=I0sinωt then calculate maximum current in the square loop.

To calculate current flowing in the square loop we have to calculate emf induced in the loop and for that we need magnetic flux linked with the square loop in terms of current flowing in the wires.

Let us select a segment at a distance x of width dx, from left wire. Distance of this segment from right wire becomes (3a-x).
Area of this selected segment is adx and magnetic field at its site can be written as follows:
B=μ0I2πx+μ0I2π(3a−x)
Magnetic fields due to both the wires are added due to same directions. Magnetic flux linked with the segment can be written as follows:
dϕ=B(adx)=[μ0I2πx+μ0I2π(3a−x)]adx
⇒dϕ=μ0Ia2π[1x+1(3a−x)]dx
Total flux linked with the square loop can be calculated by integrating above relation.
ϕ=μ0Ia2π∫2aa[1x+1(3a−x)]dx
⇒ϕ=μ0Ia2π[Inx - In(3a - x)]2aa
⇒ϕ=μ0Ia2π[{In 2a - In(3a - 2a)}−{Ina - In(3a - a)}]
⇒ϕ=μ0Ia2π[In 2a - In(a) -In(a) - In(2a)]
⇒ϕ=μ0Iaπ[In 2a - In(a)]
⇒ϕ=μ0Iaπ[In2aa]
⇒ϕ=μ0IaπIn2
Current flowing in the winesis given by I=I0sinωt and hence flux can be written as follows:
⇒ϕ=μ0I0aIn2πsinωt
emf induced in the square loop can be calculated by finding rate of change of magnetic flux. So, emf induced in the square loop can be written as
⇒ε=−dϕdt=−μ0I0aIn2πωcosωt
Charge stored in the capacitor as a function of time can be written as follows:
⇒q=Cε=−μ0CI0aωIn2πcosωt
Hence magnitude of instantaneous current can be written as
i=dqdt=μ0CI0aω2In2πsinωt
From above equation maximum current flowing in the circuit can be written as follows:
imax=μ0CI0aω2In2π
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT TEXTBOOK EXERCISE)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT ADDITIONAL EXERCISE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
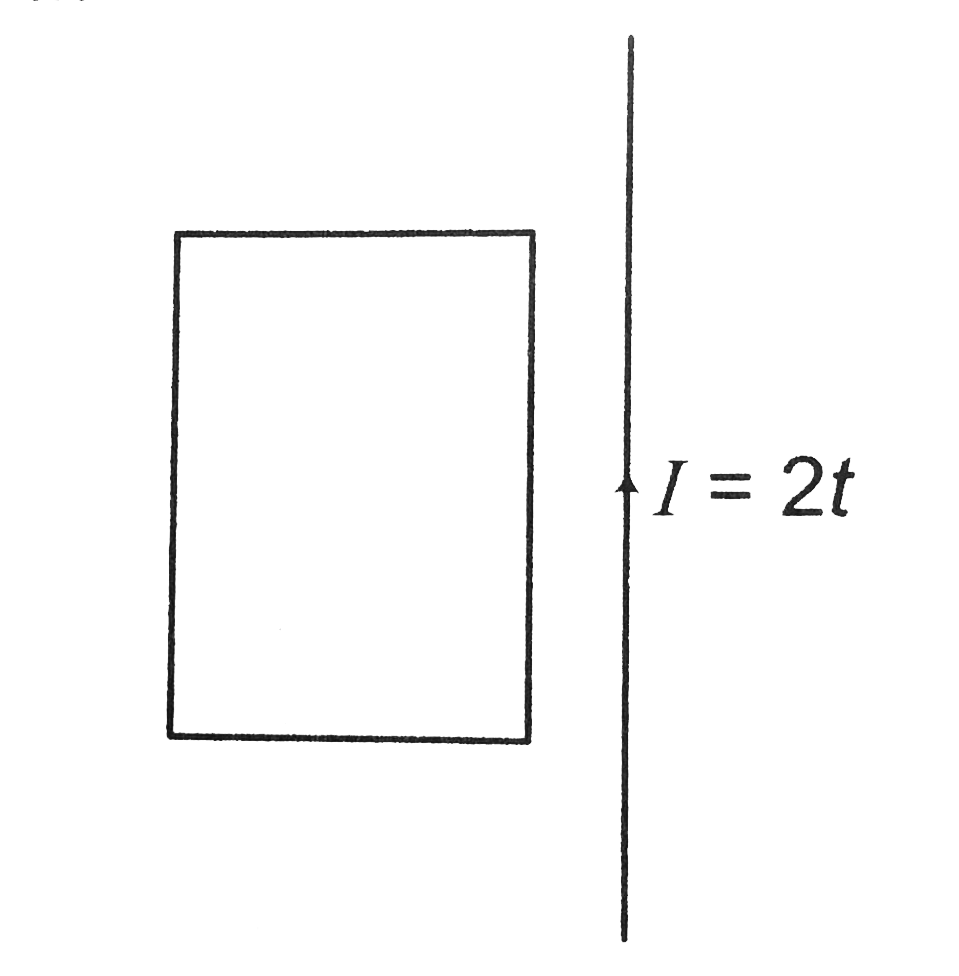
A rectangular loop is placed to the left of large current carrying straight wire as shown in Figure. Current varies with time as I=2t. Find direction of induced current Iin in the square loop.
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View Solution
Knowledge Check
A loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
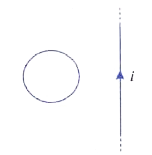 AclockwiseBanticlockwiseCzeroDcannot determine
AclockwiseBanticlockwiseCzeroDcannot determineA rectangular loop is placed to the left of large current carrying straight wire as shown in Figure. Current varies with time as I=2t. Find direction of induced current Iin in the square loop.
 Ain complete informationBNot inducedCAnticlockwiseDClockwise
Ain complete informationBNot inducedCAnticlockwiseDClockwiseA long straight wire is parallel to one edge of a rectangular loop as shown in figure-5.310. if the current in the long wire varies with time as I=I0e−tr, what will be the induced emf in the loop at t=τ?
 Aμ0bIπτIn(d+ad)Bμ0bI2πτIn(d+ad)C2μ0bIπτIn(d+ad)Dμ0bIπτIn(dd+a)
Aμ0bIπτIn(d+ad)Bμ0bI2πτIn(d+ad)C2μ0bIπτIn(d+ad)Dμ0bIπτIn(dd+a)
A rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
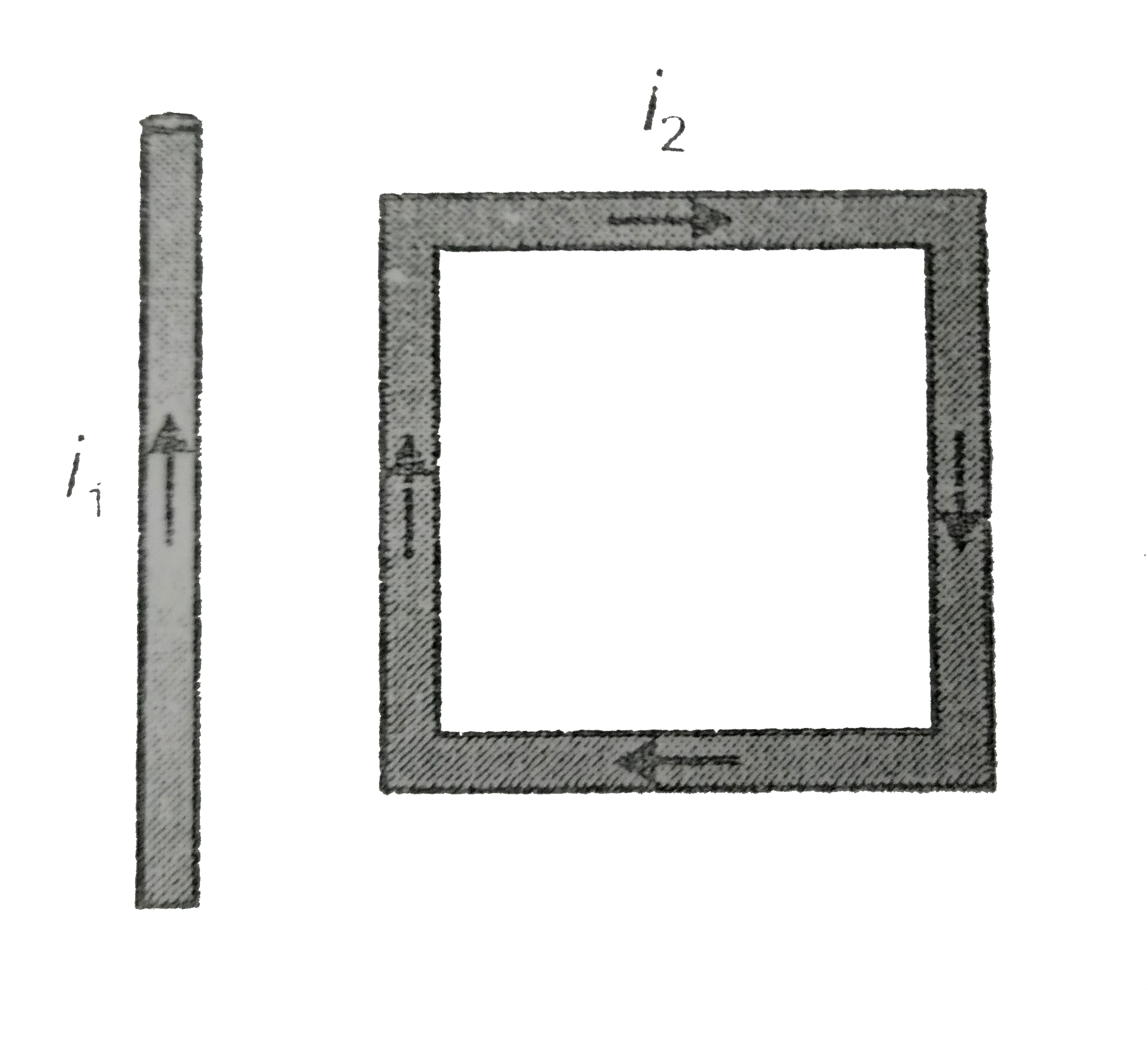
View SolutionA rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will

View SolutionFigure shows a long straight wire carrying current I and a square conducting wire loop of side l, at a distance 'a' from current wire. Both the current wire and loop are in the plane of paper. Find the flux of magnetic filed of current wire, passing through the loop.

View SolutionA long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
View SolutionA square loop of side a carries a current I. The magnetic field at the center of the loop is
View Solution
