There are two fixed infinite vertical conducting plates M and N which are kept parallel to each other at a separation 2r. At one end plates are connected through a resistor of resistance R. Uniform magnetic field B is applied perpendicular to the plane as shown in figure. A metal ring of radius r falls vertically between the plates in such a manner that plates are always along tangent to ring. Plate M is sufficiently rough but plate N to smooth. There is no slipping between plate M and ring. Resistances of ring and plates are to be neglected.

At t=0 ring us released from rest. Find the current through resistor as a function of time. Also find terminal velocity acquired by ring.

When ring is released from rest, then it starts rolling down due to sufficient friction in plate M. Pure rolling in a case of pure rotation about the point of contact on plate M. Hence for motional emf we can consider the ring as a rod of length 2r rotating about its end. If v in velocity of centre of mass of ring at some instant then angular velocity about the point of contact can be taken as v/r. When a rod of length l rotates about its end with angular velocity ω in a magnetic field perpendicular to its plane of rotation, then motional emf generated across its ends can be written as follows:
ε=12Bωl2
Hence motional emf generated due to rolling of ring between the plates can be written as
ε=12B(vr)(2r)2
ε=2Bvr
Hence, current flowing though the resistor or ring can be written as follows:
i=εR
⇒i=2BvrR ...(i)
Total current i will flow through the ring from plate M towards plate N and we know that force on current carrying wire in uniform magnetic field is independent of shape of wire and hence we can assume the ring to be a straight of length 2r carrying current i from left to right. Hence vertically upward magnetic force acting on the ring can be written as follows:
Fm=i(2r)B
Substituting value of current from equation (i). We get the following:
Fm=(2BvrR)(2r)B
Fm=4B2r2Rv ...(ii)
If a is acceleration of centre of mass of ring at some instant then its angular acceleration about the centre would be α=a/r. Applying τ=Iα about the centre of mass we get the following (see figure):
fr=Iα
Here I is moment of the inertia of the ring about centre and α=a/r.
⇒fr=mr2ar
fr=ma ...(iii)
Applying Newton.s law of motion for vertical translation of ring we get the following:
Mg−f−Fm=ma
Substituting from equation (ii) and (iii) we get the following:
Mg−ma−4B2r2Rv=ma
⇒2ma=Mg−4B2r2Rv
⇒2mRa=MgR−4B2r2v
⇒2mRdvdt=MgR−4B2r2v
⇒dvMgR−4B2r2v=dt2mR
⇒∫v0dvMgR−4B2r2v=12mR∫t0dt
⇒[−14B2r2In(MgR−4B2r2v)]v0=t2mR
⇒[In(MgR−4B2r2v)]v0=−2B2r2mRt
⇒InMgR−4B2r2vMgR=−2B2r2mRt
MgR−4B2r2vMgR=e−2B2r2mRt
⇒MgR−4B2r2v=MgRe−2B2r2mRt
⇒4B2r2=MgR(1−e−2B2r2mRt)
⇒v=MgR4B2r2(1−e−2B2r2mRt) ...(iv)
Now we can substitute velocity as a function of time in equation (i) to get the current as function of time.
i=2BrRMgR4B2r2(1−e−2B2r2mRt)
⇒i=Mg2Br(1−e−2B2r2mRt) ...(v)
From equation (iv) we can see that ring will attain terminal velocity after a long time and the same can be written as follows after substituting t=∞ in equation (iv):
⇒v=MgR4B2r2 ...(vi)
Equations (v) and (vi) are our answers to this question.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT TEXTBOOK EXERCISE)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT ADDITIONAL EXERCISE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CONCEPTUAL QUESTIONS
22 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Three identical metallic plates are kept parallel to one another at separations a and b. The outer plates are connected to the ground and the middle plate is given charge Q. Then, the charge on the right side of middle plate is

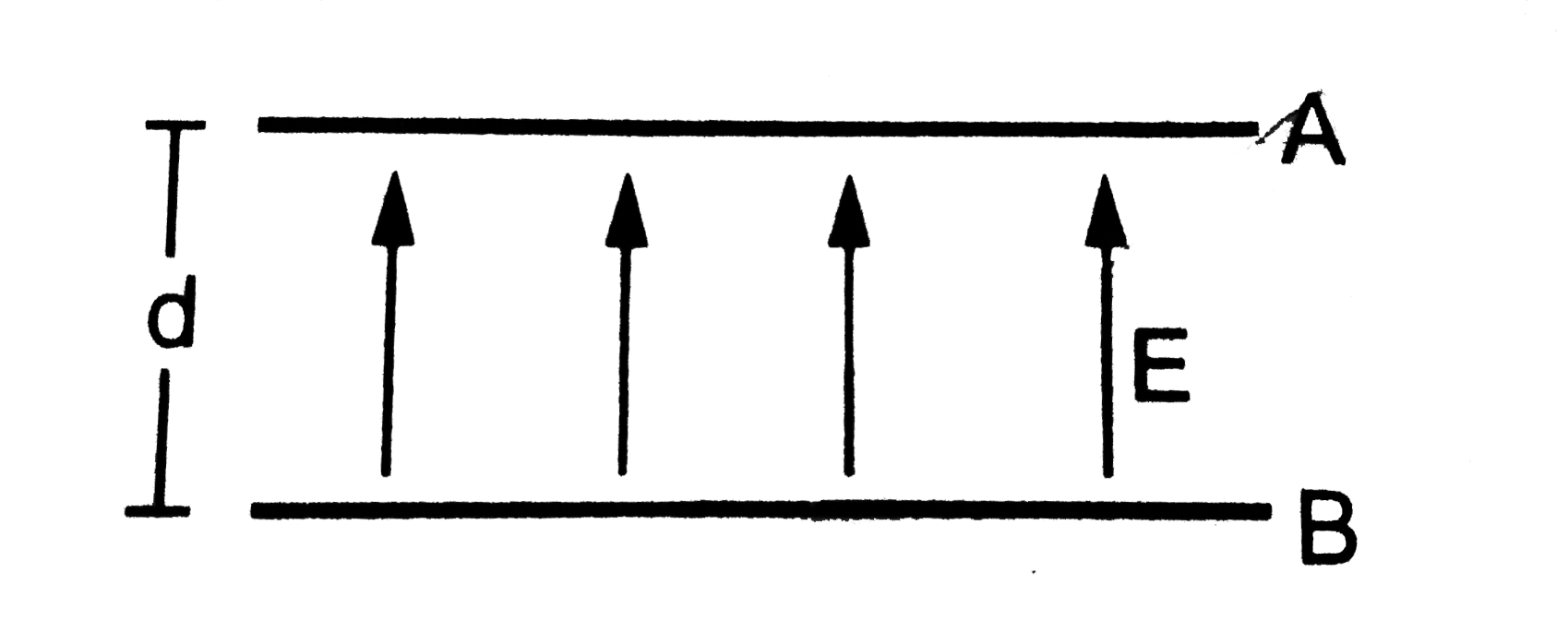
View Solutionshows two metallic plates A and B placed
. parallel to each other at a separaton d. A uniform
. electric field E exists between the plates in the direction
. from plate B to plate A. Find the potential difference
. between the plates.
View Solution
Knowledge Check
Three identical metallic plates are kept parallel to one another at separations a and b. The outer plates are connected to the ground and the middle plate is given charge Q. Then, the charge on the right side of middle plate is
 AQ/2B−Qba+bCQba+bDQaa+b
AQ/2B−Qba+bCQba+bDQaa+bA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
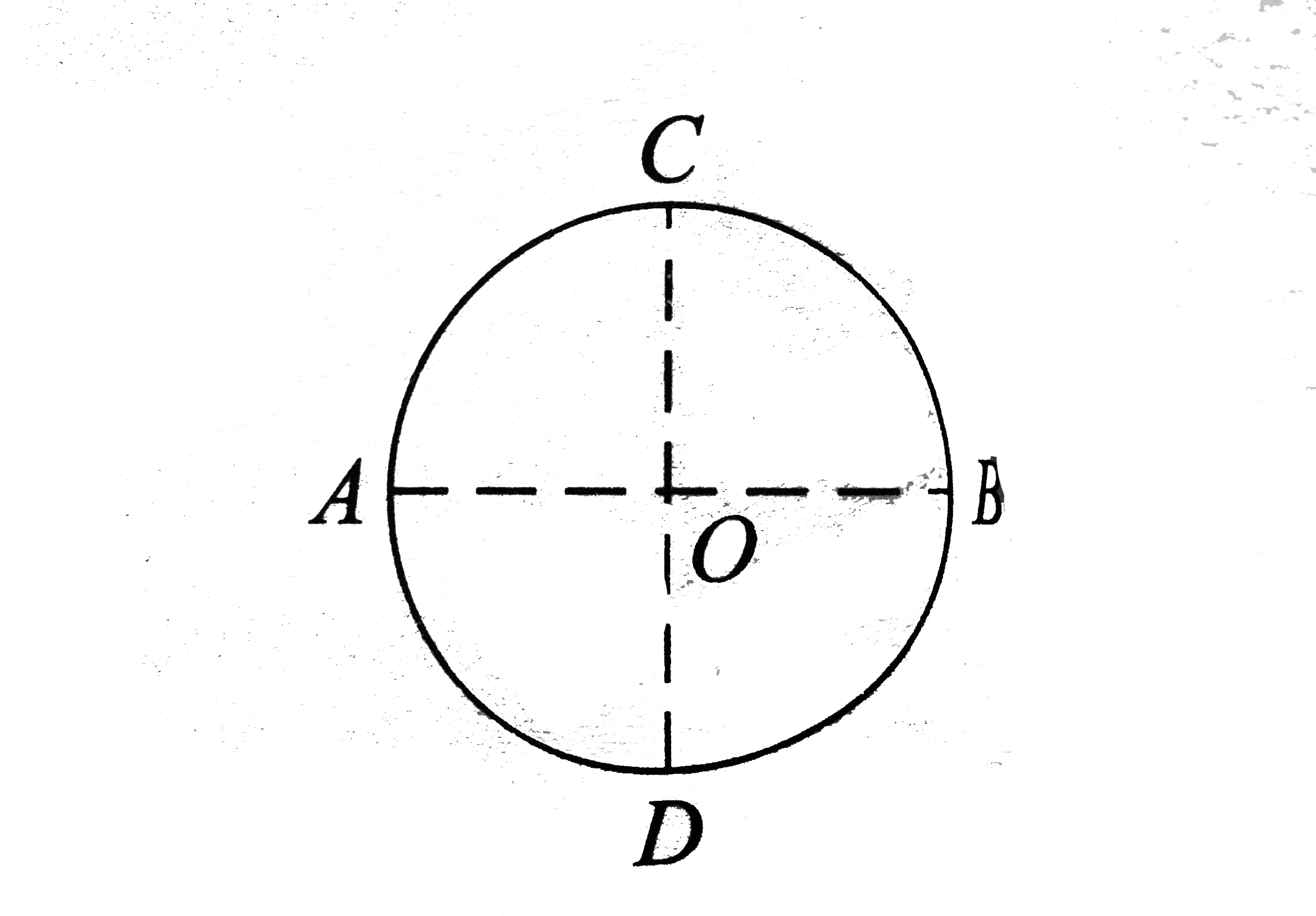 A(a) AandB are at the same potentialB(b) CandD are at the same potentialC( c) current flows in clockwise directionD( d) current flows in anticlockwise direction
A(a) AandB are at the same potentialB(b) CandD are at the same potentialC( c) current flows in clockwise directionD( d) current flows in anticlockwise direction
Three identical metallic plates are kept parallel to one another at separations a & b as shown in figure. The outer plates are connected by a thin conducting wire and a charge Q is placed on the central plate. Find the charge on all the six sufaces.
View SolutionFigure shows two metallic plates A and B placed parallel to each other at a seperation d. A uniform electric field E exists between the plates in the direction from plate B to plate A. Find the potential difference between the plates.

View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
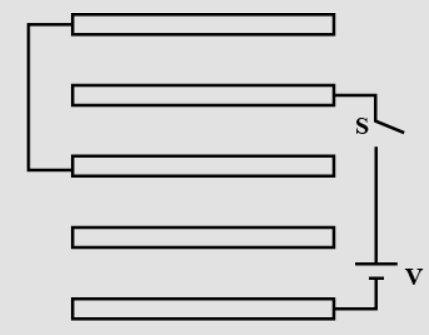
View Solution5 identical thin conducting, plates are kept parallel to each other such that separation between each plate is d.Area of each plate is A.Plates are arranged as shown in figure.All wires are conducting.Switch S is closed,find the work done bybattery. (A>>>d2)
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
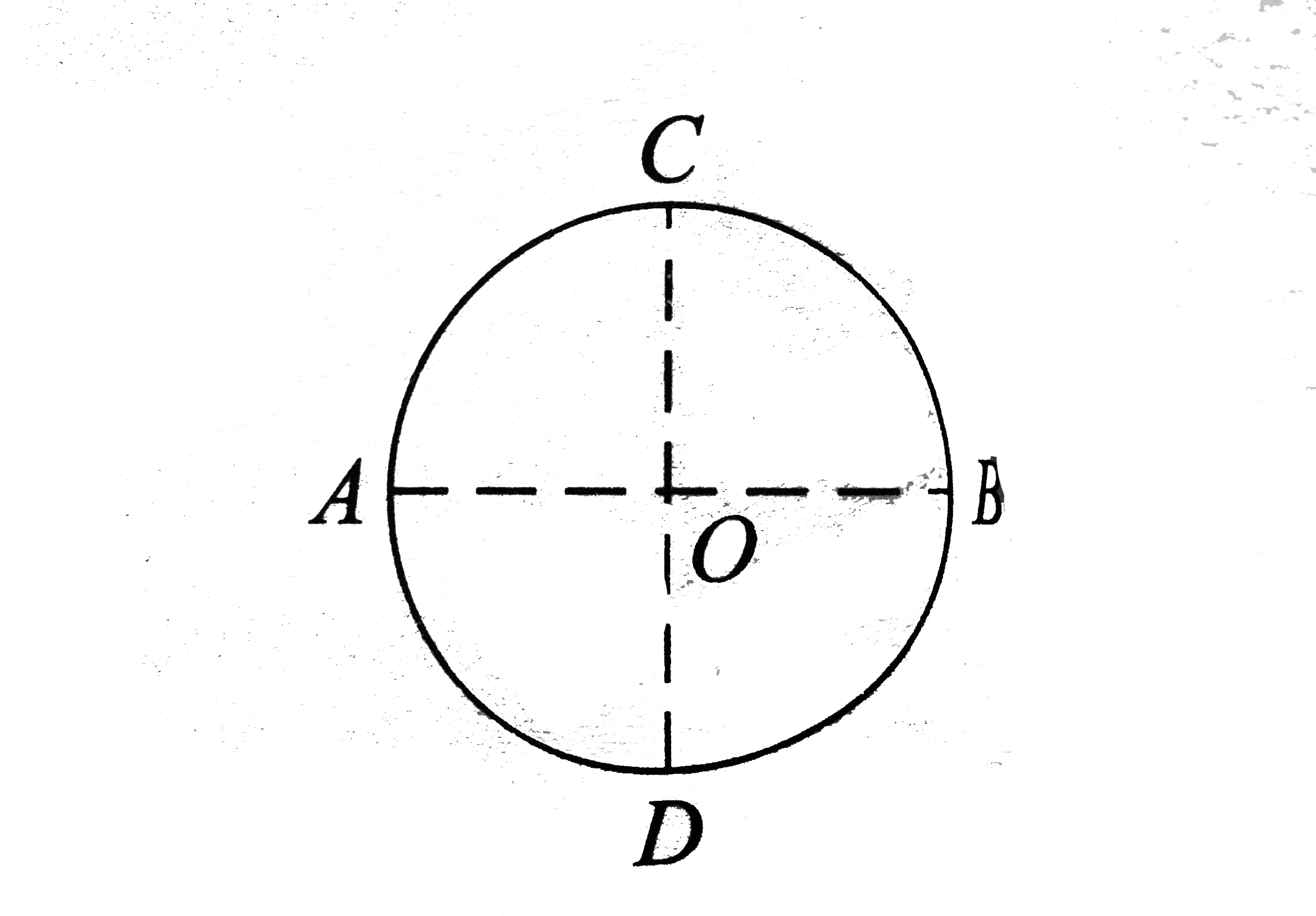
View Solution
