A square loop of a conducting material of side l and resistance r is dragged through a uniform magnetic field B with uniform velocity v keeping the plane of the loop perpendicular to the direction of the field. What is the current flowing through the loop?
To solve the problem of finding the current flowing through a square loop of conducting material being dragged through a uniform magnetic field, we can follow these steps:
Step 1: Understand the setup
We have a square loop of side length l and resistance r moving with a uniform velocity v through a uniform magnetic field B. The plane of the loop is perpendicular to the direction of the magnetic field.
Step 2: Determine the magnetic flux
The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A
where A is the area of the loop. For a square loop, the area A is:
A=l2
Thus, the magnetic flux becomes:
Φ=B⋅l2
Step 3: Analyze the motion of the loop
As the loop is dragged through the magnetic field, the area of the loop that is within the magnetic field changes. When the loop is completely inside the magnetic field, the magnetic flux is constant. However, as the loop starts to exit the magnetic field, the effective area exposed to the magnetic field decreases.
Step 4: Calculate the induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF (E) in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
When the loop is moving out of the magnetic field, the change in flux can be expressed as:
E=−B⋅dAdt
Since the area A is changing as the loop exits the field, we can express dAdt as:
dAdt=l⋅v
Thus, the induced EMF becomes:
E=−B⋅l⋅v
Step 5: Calculate the current flowing through the loop
Using Ohm's law, the current I flowing through the loop can be calculated as:
I=Er
Substituting the expression for induced EMF:
I=−B⋅l⋅vr
Since current is a scalar quantity, we can ignore the negative sign (it indicates the direction of current flow):
I=B⋅l⋅vr
Final Answer
The current flowing through the loop is:
I=B⋅l⋅vr
We have a square loop of side length l and resistance r moving with a uniform velocity v through a uniform magnetic field B. The plane of the loop is perpendicular to the direction of the magnetic field.
The magnetic flux Φ through the loop is given by the formula:
Φ=B⋅A
where A is the area of the loop. For a square loop, the area A is:
A=l2
Thus, the magnetic flux becomes:
Φ=B⋅l2
As the loop is dragged through the magnetic field, the area of the loop that is within the magnetic field changes. When the loop is completely inside the magnetic field, the magnetic flux is constant. However, as the loop starts to exit the magnetic field, the effective area exposed to the magnetic field decreases.
According to Faraday's law of electromagnetic induction, the induced EMF (E) in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
When the loop is moving out of the magnetic field, the change in flux can be expressed as:
E=−B⋅dAdt
Since the area A is changing as the loop exits the field, we can express dAdt as:
dAdt=l⋅v
Thus, the induced EMF becomes:
E=−B⋅l⋅v
Using Ohm's law, the current I flowing through the loop can be calculated as:
I=Er
Substituting the expression for induced EMF:
I=−B⋅l⋅vr
Since current is a scalar quantity, we can ignore the negative sign (it indicates the direction of current flow):
I=B⋅l⋅vr
The current flowing through the loop is:
I=B⋅l⋅vr
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Additional Questions (Carrying I mark))
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Fill in the blanks)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - HIGHER ORDER THINKING SKILLS AND ADVANCED LEVEL
8 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Knowledge Check
A square loop of side L, resistance R placed in a uniform magnetic field B acting normally to the plane of the loop. If we attempt to pull it out of the field with a constant velocity v, then the power needed is
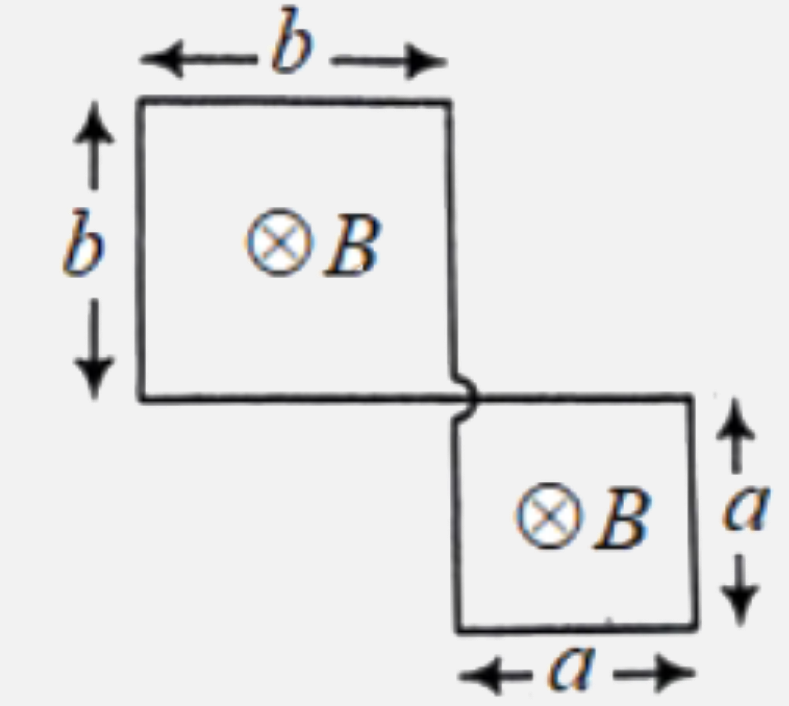
ABRlvBB2l2v2RCBl2v2RDBvlRA conducting square loop edge length a and resistance R is in a uniform magnetic field B, perpendicularly. Two opposite corners of the loop are pulled apart as shown in fig., till it becomes straight, the charge flown through the loop will be -
 ABa2RB2Ba2RCBa22RDZero
ABa2RB2Ba2RCBa22RDZeroA rectangular loop of resistance R, and sides l and X, is pulled out of a uniform magnetic field B with a for maintaining uniform velocity of withdrawal is __
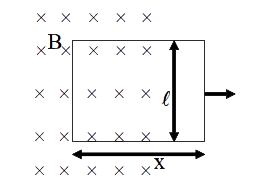 ABl2vRBB2l2vRCB2l2v2RD0
ABl2vRBB2l2vRCB2l2v2RD0
A conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is

View SolutionA conducting loop in the form of a circule is placed in a uniform magnetic field with its place perpendicular to the direction of the field. An e.m.f. will be induced in the loop if
View SolutionA conducting circular loop of radius r carries a constant current i.It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is
View SolutionA conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field→B such that vecB is perpendicular to the plane of the loop. What is the torque acting on the loop?
View Solution