Steady current i flowing through a solenoid, whose core is made with a material of permeability μ. If core of the solenoid is abruptly removed then what current will flow through the circuit just after core is removed.
μi0
i0μ
i0
0
The correct Answer is:A
To solve the problem of determining the current flowing through a circuit just after the core of a solenoid is removed, we can follow these steps:
1. Understand the Initial Condition:
- A steady current i0 is flowing through the solenoid when the core (with permeability μ) is present. The self-inductance of the solenoid is L.
2. Identify the Change When the Core is Removed:
- Upon removing the core, the self-inductance changes. The new self-inductance L′ of the solenoid without the core can be expressed as:
L′=Lμ
3. Magnetic Flux Relation:
- The magnetic flux Φ through the solenoid is related to the self-inductance and the current:
Φ=L⋅i
- Initially, with the core, the magnetic flux is:
Φ1=L⋅i0
- After removing the core, the magnetic flux is:
Φ2=L′⋅i
4. Equate the Magnetic Flux Before and After:
- Since the magnetic flux must remain continuous (i.e., Φ1=Φ2), we can set up the equation:
L⋅i0=L′⋅i
5. Substitute the Expression for L′:
- Substitute L′ into the equation:
L⋅i0=(Lμ)⋅i
6. Solve for the Current i:
- Rearranging the equation gives:
i=L⋅i0⋅μL
- Simplifying this, we find:
i=μ⋅i0
Final Result:
The current flowing through the circuit just after the core is removed is:
i=μ⋅i0
- A steady current i0 is flowing through the solenoid when the core (with permeability μ) is present. The self-inductance of the solenoid is L.
- Upon removing the core, the self-inductance changes. The new self-inductance L′ of the solenoid without the core can be expressed as:
L′=Lμ
- The magnetic flux Φ through the solenoid is related to the self-inductance and the current:
Φ=L⋅i
- Initially, with the core, the magnetic flux is:
Φ1=L⋅i0
- After removing the core, the magnetic flux is:
Φ2=L′⋅i
- Since the magnetic flux must remain continuous (i.e., Φ1=Φ2), we can set up the equation:
L⋅i0=L′⋅i
- Substitute L′ into the equation:
L⋅i0=(Lμ)⋅i
- Rearranging the equation gives:
i=L⋅i0⋅μL
- Simplifying this, we find:
i=μ⋅i0
The current flowing through the circuit just after the core is removed is:
i=μ⋅i0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (AIPMT/NEET & Other State Boards for Medical Entrance)
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (JEE (Main) & Other State Boards for Engineering Entrance)
38 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - REVISION EXERCISE (Numerical Problems)
16 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Knowledge Check
Total current flowing through the circuit:
 A0.677 AB0.057 AC0.87 AD2.87 A
A0.677 AB0.057 AC0.87 AD2.87 AMaterials wich allow larger currents to fow through them are called
AConductorBInsulatorCGlassDPlasticA steady electric current is flowing through a cylindrical conductor. Then,
Athe electric field at the axis of the conductor is zeroBthe magnetic field at the axis of the conductor is zeroCthe electric field in the vicinity of the conductor is zeroDthe magnetic field in the vicinity of the conductor is zero
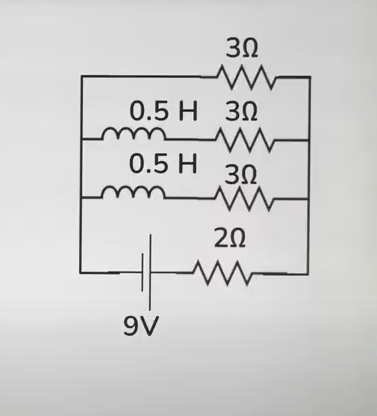
Find the current flowing through the battery in steady state?
View SolutionIn the circuit, the current flowing through the zener diode is
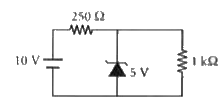
View SolutionThe direction of the flow of current through electric circuit is
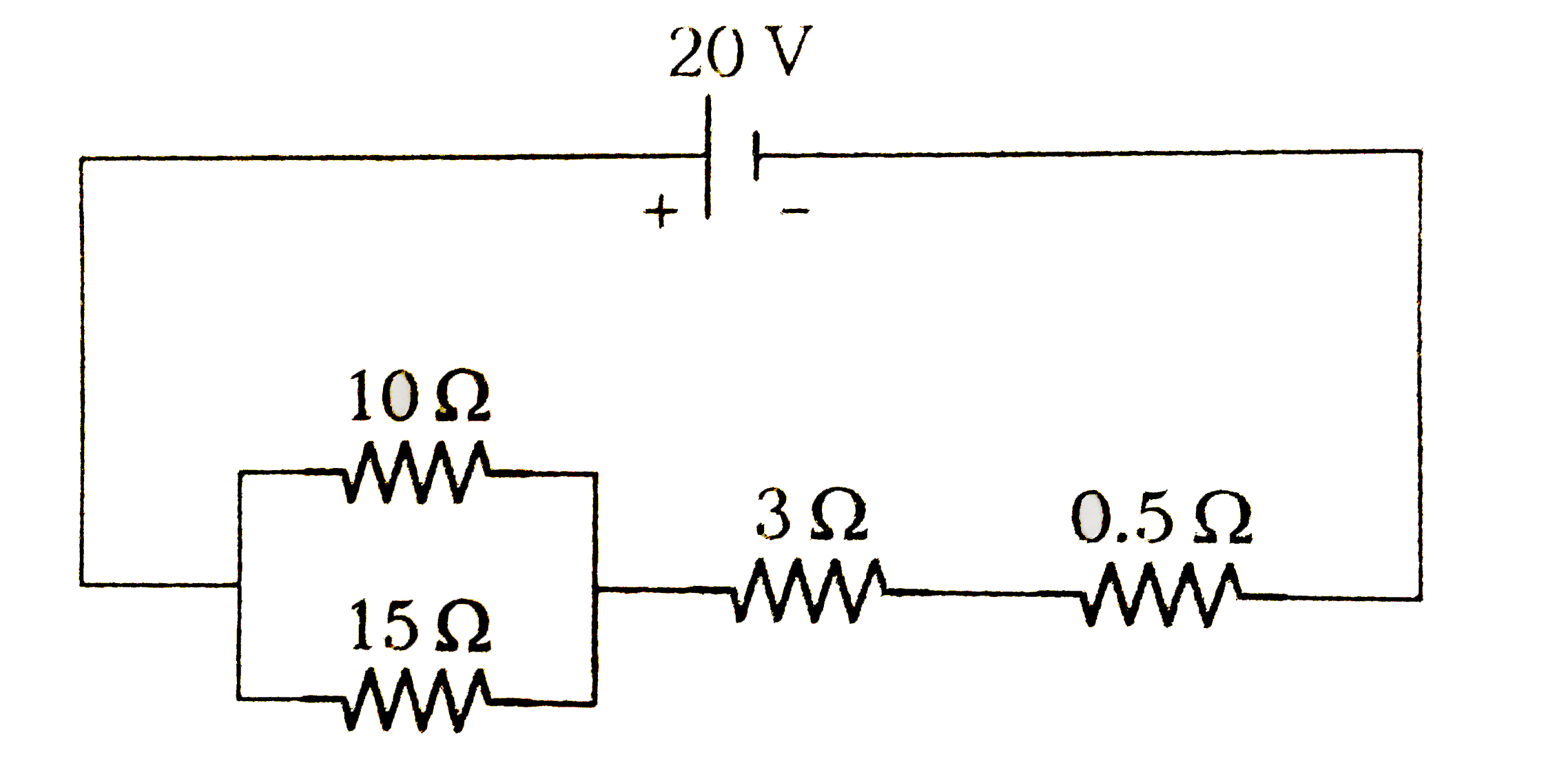
View SolutionIn the circuit, the current flowing through 10Ω resistance is
View SolutionA current of 1.6 A flows through a long solenoid, having 8 turns/cm. The magnetic induction at the end of the solenoid along its axis is
View Solution


