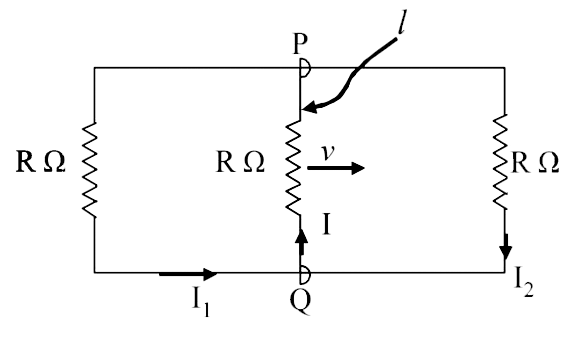
A rectangular loop has a sliding connector PQ of length I and resistance RΩ and it is moving with a speed v as shown.

The set-up is placed in a uniform magnetic field B going into the plane of the paper. The three currents I1,I2 and I are:
I1=I2=Bl16R,I=Blv3R
I1=−I2=BlvR,I=2BlvR
I1=I2=Blv3R,I=2Blv3R
I=I2=I=blvR
The correct Answer is:C

Branch PQ will induce emf by Fleming.s right-hand rule.
Apply KVL in loop I
−I1R−IR+ε=0 ...(i)
Apply KVL in loop II
−I2R−IR+ε=0 ...(ii)
On adding (i) and (ii)
−R(I1+I2)−2IR+2ε=0 ∴I=I1+I2
−IR−2IR+2ε=0
I=2ε3R
The emf indiced in wire PQ
ε=Bvl
And current, I=2Bvl3R
The above diagram shows that I1 and I2 are symmetric, so current in both branches will be same.
I1=I2
∴I=I1+I2=2I1=2I2
I2=I1=Bvl3R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS BASED ON GIVEN PASSAGE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (AIPMT/NEET & Other State Boards for Medical Entrance)
8 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A rectangular loop has a sliding connector PQ of length l and resistance R(Ω) and it is moving with a speed v as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents I1,I2 and I are
View SolutionA rectangular loop has a sliding connector PQ of length l and resistance R(Ω) and it is moving with a speed v as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents I1,I2 and I are

View Solution
Knowledge Check
A rectangular loop has a sliding connector PQ of length l and resistance R(Ω) and it is moving with a speed v as shown. The set-up is placed in a uniform magnetic field going into the plane of the paper. The three currents I1,I2 and I are
 AI1=−I2=Blv6R,I=2Blv6RBI1=I2=Blv3R,I=2Blv3RCI1=I2=I=BlvR,DI1=I2=Blv6R,I=Blv3R
AI1=−I2=Blv6R,I=2Blv6RBI1=I2=Blv3R,I=2Blv3RCI1=I2=I=BlvR,DI1=I2=Blv6R,I=Blv3RA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
 AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξs
AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξsA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
Ais zero only for one orientation of loop in magnetic fieldBis zero for two symmetricaly located positions of loop in magnetic fieldCis zero for all orientationsDis never zero
A conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View SolutionA rectangular loop PQMN with movable arm PQ of length 10 cm and resistance 2Ω is placed in a uniform magnetic field of 0.1 T acting perpendicular to the plane of the loop as shown in Fig. 6.37. The resistance of the arm MN, NP and MQ are negligible. Calculate (i) the emf induced in the arm PQ, and (ii) current induced in the loop when arm PQ is moved with velocity 20ms−1.

View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View Solution
