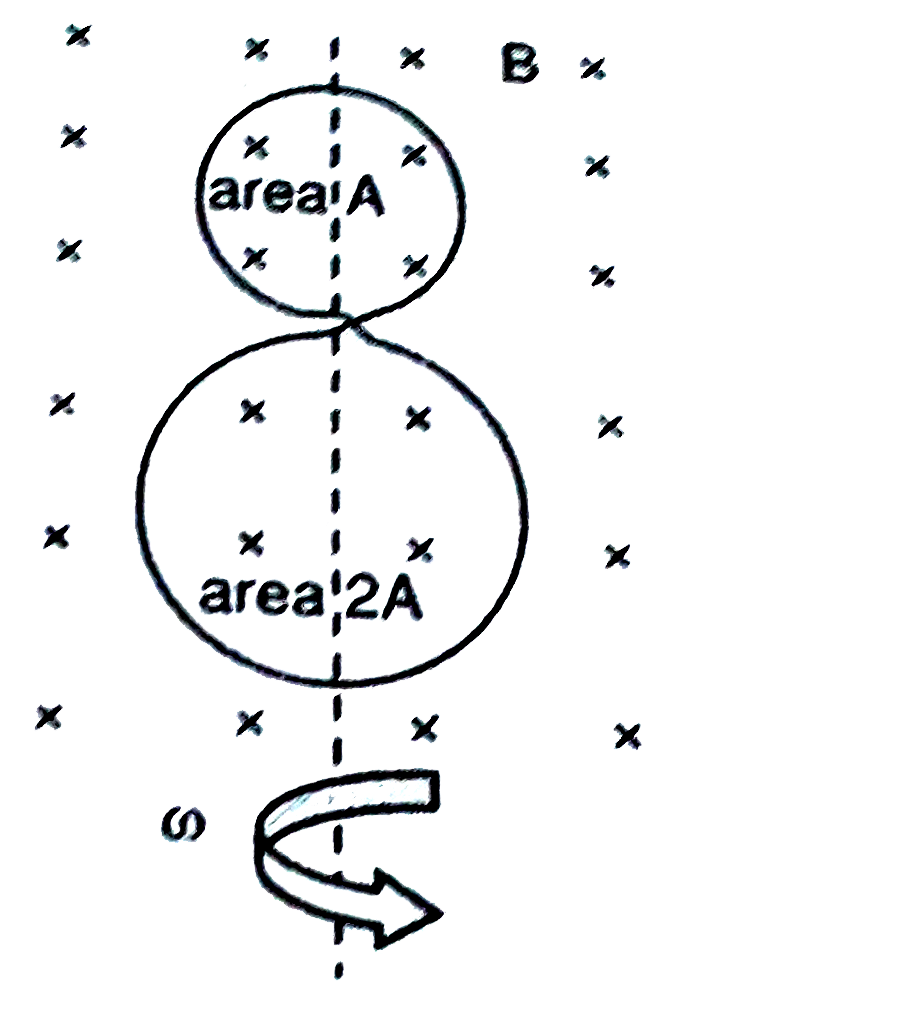
A circular insulated copper wire loop is twisted to form two loops of area A and 2 A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane (of the paper). A uniform magnetic field points into the plane of the paper. At t = 0, the loop starts area:A rotation ebout the common diameter as I , axis with a constant : angular velocity in the magnetic field. Which of the following options is/are correct?

The net emf induced due to both the loops is proportional to
The rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paper.
The amplitude of the maximum net emf induced due to both the loops is equal to the amplitude of maximum emf induced in the smaller loop alone.
The emf induced in the loop is proportional to the sum of the area of the two loops
The correct Answer is:B, C
If we assume initial angle between area vector and magnetic field to be zero, then angle between them after time t is , where is angular speed. Flux can be written us
Here A. is area of coil.
Hence, option (a) is wrong.
is maximum when , hence when plane of the loop is perpendicular to plane of paper. Hence, option (b) is correct.
To calculate emf in smaller loop only, we can put A. = A. But when we talk about complete loop then we should know that directions of current in the two parts are opposite to each other. Hence for the net flux we can effectively take A. = 2 A-A-A. Hence we can see that is same in the above two cases. So option (c) is correct.
in the above discussion we have already discussed that net area vector is equal to difference of the two parts, hence option (d) is wrong.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS BASED ON GIVEN PASSAGE)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (ASSERTION REASON TYPE QUESTIONS)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - COMPETITION FILE (MULTIPLE CHOICE QUESTIONS) (AIPMT/NEET & Other State Boards for Medical Entrance)
8 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
A circular insulated copper wire loop is twisted to form two loops of are A and 2A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane ( of the paper). A uniform magnetic →B point into the plane of the paper . At t=0, the loop starts rotation about the common diameter as axis with a constant angular velocity ω in the magnetic field. Which of the following options is /are correct ?
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to

View Solution
Knowledge Check
A circular insulated copper wire loop is twisted to form two loops of are A and 2A as shown in the figure. At the point of crossing the wires remain electrically insulated from each other. The entire loop lies in the plane ( of the paper). A uniform magnetic →B point into the plane of the paper . At t=0, the loop starts rotation about the common diameter as axis with a constant angular velocity ω in the magnetic field. Which of the following options is /are correct ?
 AThe net emf induced due to both the loops is proportional to cosωtBThe rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paperCThe amplitude of the maximum net emf induced due to both the loops is equl to the amplitude of maximum emf induced in the smaller loop aloneDThe emf indued in the loop is proportional to the sum of the area of the two loops.
AThe net emf induced due to both the loops is proportional to cosωtBThe rate of change of the flux is maximum when the plane of the loops is perpendicular to plane of the paperCThe amplitude of the maximum net emf induced due to both the loops is equl to the amplitude of maximum emf induced in the smaller loop aloneDThe emf indued in the loop is proportional to the sum of the area of the two loops.A conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
 AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξs
AcontractBexpandCmove towards +vex−aξsDmove towards −vex−aξsA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is
 ABiRBBIR2C2BIRDZero
ABiRBBIR2C2BIRDZero
A circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
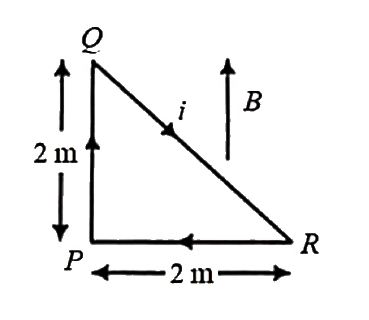
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is

View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View Solution
