Current flowing through an inductor as a function of time is given as follows :
I = 4 + 16 t. here I is in amperes and t is in seconds. Emf induced in the inductor is 20 mV.
What is self-inductance of the inductor ?
1.25 ×10−3 H
2.5×10−4 H
1.25×10−4 H
5×10−3 H
The correct Answer is:A
To find the self-inductance L of the inductor given the current I as a function of time and the induced EMF, we can follow these steps:
Step 1: Identify the given information
We are given:
- The current I(t)=4+16t (in amperes)
- The induced EMF E=20mV=20×10−3V
Step 2: Calculate the rate of change of current
To find the self-inductance, we need to calculate didt. We differentiate the current function I(t):
didt=ddt(4+16t)=16A/s
Step 3: Use the formula for induced EMF
The induced EMF in an inductor is given by the formula:
E=−Ldidt
Since we are interested in the magnitude, we can drop the negative sign:
E=Ldidt
Step 4: Substitute the known values into the equation
Now we can substitute the values we have:
20×10−3=L⋅16
Step 5: Solve for self-inductance L
Rearranging the equation to solve for L:
L=20×10−316
Calculating this gives:
L=1.25×10−3H
Step 6: Final answer
Thus, the self-inductance of the inductor is:
L=1.25mH (milliHenries)
We are given:
- The current I(t)=4+16t (in amperes)
- The induced EMF E=20mV=20×10−3V
To find the self-inductance, we need to calculate didt. We differentiate the current function I(t):
didt=ddt(4+16t)=16A/s
The induced EMF in an inductor is given by the formula:
E=−Ldidt
Since we are interested in the magnitude, we can drop the negative sign:
E=Ldidt
Now we can substitute the values we have:
20×10−3=L⋅16
Rearranging the equation to solve for L:
L=20×10−316
L=1.25×10−3H
Thus, the self-inductance of the inductor is:
L=1.25mH (milliHenries)
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE ASSERTION REASON TYPE QUESTIONS
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE INTEGER TYPE QUESTIONS
11 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE C. MULTIPLE CHOICE QUESTIONS
17 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
Find the time in which the current changes from 3 A to 1 A through an inductor of 10 H. The emf induced in the inductor is 20 V. Also, find the magnetic flux linked with the inductor.
View SolutionIn an inductor, the current / varies with time to l=5A+16.(A/s)t. If-induced emf in the induct is 5 mV, the self inductance of the inductor is
View Solution
Knowledge Check
Current flowing through an inductor as a function of time is given as follows :
I = 4 + 16 t. here I is in amperes and t is in seconds. Emf induced in the inductor is 20 mV.
Rate of energy supplied to inductor at t = 2 s isA0.36 WB0.72 WC1.44 WD2.88 WThe current in a 90mH inductor changes with time as i=1.0t2, where I is in amperes and t is in seconds.
Athe magnitude of the induced emf at t=4.0s is 180 mVBthe emf zero at time t=3.0sCthe magnitude of the induced emf at t=4.0s is 360 mVDthe emf zero at time t=4.0sThe current in ampere through an inductor is
i(10+20t)
Here t is in second. The induced emf in the inductor 4V.
The self inductance of the indicator is, L…..H,A0.2B0.4C0.1D1.0
The current in ampere in an inductor is given by I=4t2+6t where is in s. The self induced e.m.f in it is 20 mV. The self inductance of the coil t=0
View SolutionThe potential difference across a 2H inductor as a function of time is shown in figure. At time t=0, current is zero
Current t=2 second is
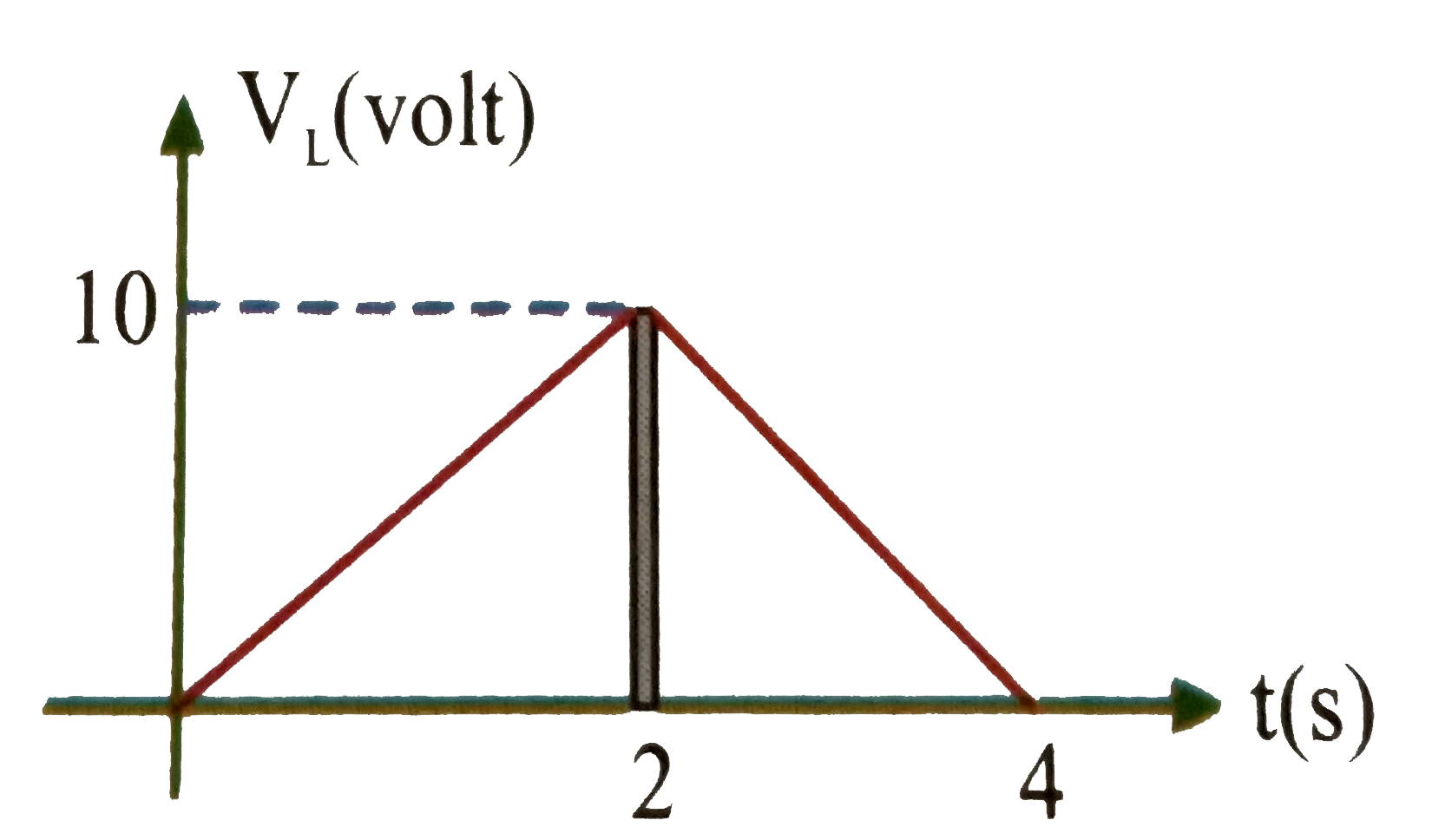
View SolutionCurrent flowing through a conducting wire is given by
I=(1+2t)
Where t is in seconds and current I is in amperes. The charge (in coulombs) flown through the resistor in the interval from t=0 to t=1 second is -
View SolutionIf a current of 10A flows in one second through a coil and the induced e.m.f. is 10V, then the self-inductance of the coil is
View SolutionThe current in ampere through an inductor is
i(10+20t)
Here t is in second. The induced emf in the inductor 4V.
Total flux linked with the inductor at t= 2 is
View Solution
