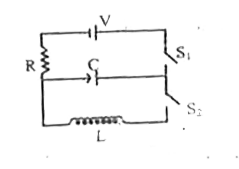
A capacitor having capacitance C can be charged (with the help of a resistor having resistance R ) by a battery of voltage V, by closing switch S1 and at the same time keeping switch S2 open. The capacitor can be connected in series with an inductor with inductance L by closing switch S2 and opening S1 .

If the total charge stored in the LC circuit is Q0, then for t > 0
The charge on the capacitor is Q = Q0 cos (π2+t√LC).
the charge on the capacitor is Q = Q0 cos (π2−t√LC).
the charge on the capacitor is Q = - LCd2Qdt2 .
the charge on the capacitor is Q = - 1√LCd2Qdt2 .
The correct Answer is:C
( c ) Charge on capacitor is Q0 at t=0 and hence options ( a ) and ( b) cannot given correct representation of charge on capacitor as a funtion iof time in the given situation.
On the other hand charge on capacitor oscillates simple harmonically which is represented in options ( c) and (d) but angular frequency of oscillation in option (C) is only correct . Angular frequency of oscillation is
1√LC .
Only option ( c) is correct.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE ASSERTION REASON TYPE QUESTIONS
10 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE INTEGER TYPE QUESTIONS
11 Videos
- ALTERNATING CURRENT BOOK - MODERN PUBLICATIONCHAPTER - ALTERNATING CURRENT EXERCISE - COMPETITION FILE C. MULTIPLE CHOICE QUESTIONS
17 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
Similar Questions
The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
Initially the capacitor was uncharged.Now switch S1 is closed and S2 is kept open.If time constant of this circuit is t, then

View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
Initially the capacitor was uncharged.Now switch S1 is closed and S2 is kept open.If time constant of this circuit is τ, then

View Solution
Knowledge Check
The capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.
If the total charge storge in the LC circuit is Q0, then for t ≥ 0Athe charge on the capacitor is Q = Q0cos(π2+t√LC)Bthe charge on the capacitor is Q = Q0cos(π2−1√LC)Cthe charge on the capacitor is Q = LC d2Qdt2Dthe charge on the capacitro is Q = - 1√LCd2Qdt2The capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor.Then
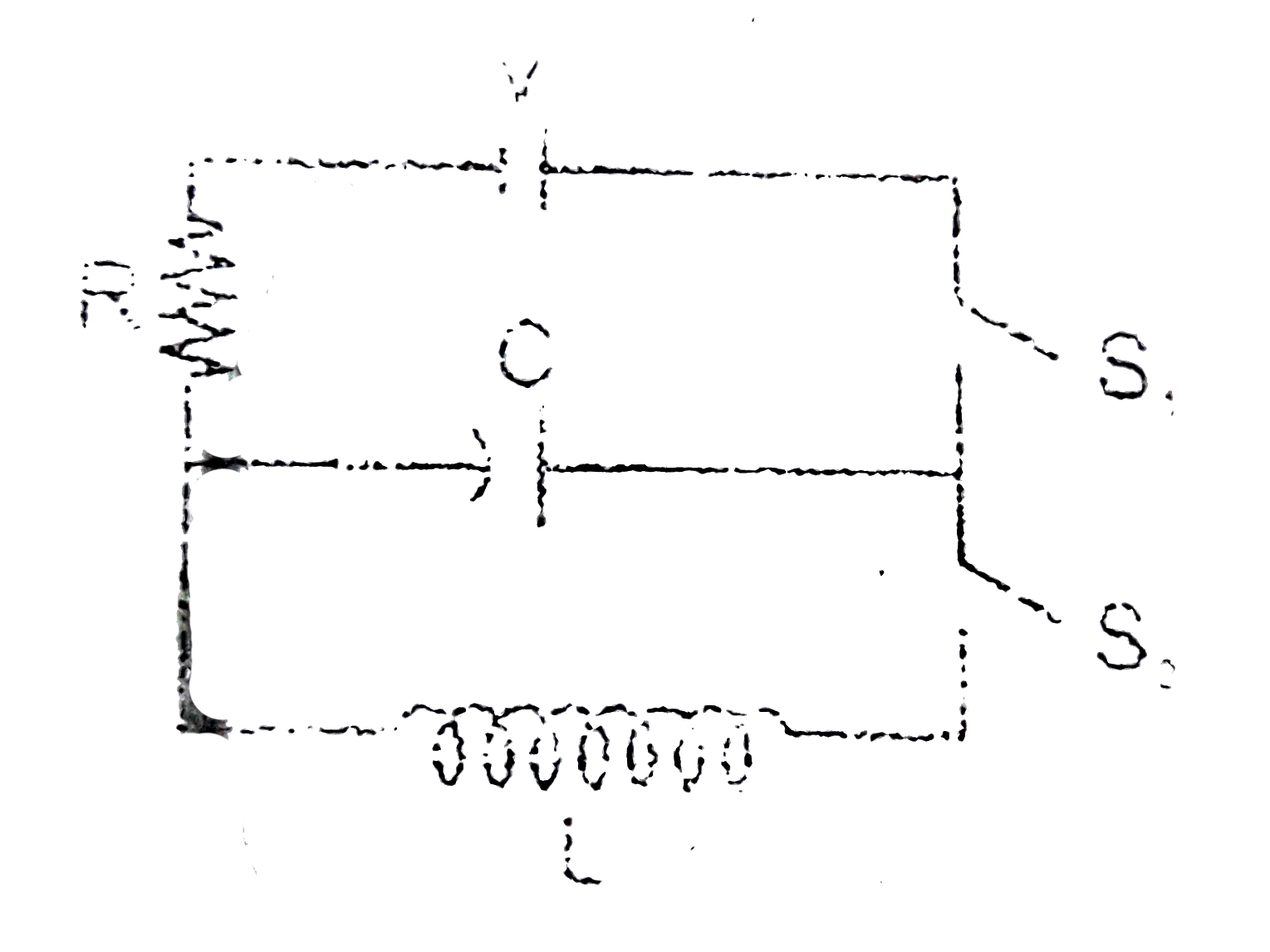 Aat t=0,energy stored in the circuit is purely in the form of magnetic energyBat any time t>0,current in the circuit is in the same directionCat t>0,there is no exchange of energy between the inductor and capacitorDat any time t>0 instanteous curren in the circuit will have maximum vlaue V√CL ,where C is the capacitance and L is the inductance.
Aat t=0,energy stored in the circuit is purely in the form of magnetic energyBat any time t>0,current in the circuit is in the same directionCat t>0,there is no exchange of energy between the inductor and capacitorDat any time t>0 instanteous curren in the circuit will have maximum vlaue V√CL ,where C is the capacitance and L is the inductance.The capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,Aat t=0, energy stored in the circuit is purely in the form of magnetic energyBat any time t<0, current in the circuit is in the same direction.Cat t>0, there is no exchange of energy between the inductor and capacitorDat any time t>0, instananeous current in the circuit will have maximum value V√CL, where C is the capacitance and L is the inductance.
The capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, then
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, then
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor ‘L’ by closing switch S2 and opening S1

After the capacitor gets fully charged, S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
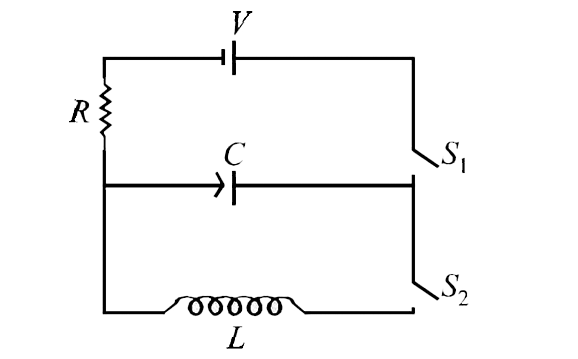
When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,
View Solution
