White light is incident on a soap film of μ=4/3 at an angle of 45∘. On examining the transmitted light with a spectrometer, a bright band of wavelength 5400Å is found. What will be the minimum thickness of the soap film?
To find the minimum thickness of the soap film that produces a bright band of wavelength 5400 Å when white light is incident at an angle of 45°, we can follow these steps:
Step 1: Understand the given data
- Refractive index of soap film, μ=43
- Angle of incidence, I=45∘
- Wavelength of light, λ=5400Å=5400×10−10m=5.4×10−7m
Step 2: Apply Snell's Law
Using Snell's law, we can find the angle of refraction R:
μ=sinIsinR
Substituting the known values:
43=sin45∘sinR
Since sin45∘=1√2:
sinR=sin45∘μ=1√243=34√2
Step 3: Calculate cosR
Using the identity cos2R+sin2R=1:
sin2R=(34√2)2=932
Thus,
cos2R=1−sin2R=1−932=32−932=2332
So,
cosR=√2332≈0.8477
Step 4: Use the formula for minimum thickness
For constructive interference in thin films, the condition is given by:
2μtcosR=nλ
For minimum thickness, we take n=1:
t=λ2μcosR
Step 5: Substitute the values to find t
Substituting the known values:
t=5.4×10−72×43×0.8477
Calculating the denominator:
2×43×0.8477≈83×0.8477≈2.259
Thus,
t≈5.4×10−72.259≈2.39×10−7m
Final Answer
The minimum thickness of the soap film is approximately:
t≈2.39×10−7m or 239nm
---
- Refractive index of soap film, μ=43
- Angle of incidence, I=45∘
- Wavelength of light, λ=5400Å=5400×10−10m=5.4×10−7m
Using Snell's law, we can find the angle of refraction R:
μ=sinIsinR
Substituting the known values:
43=sin45∘sinR
Since sin45∘=1√2:
sinR=sin45∘μ=1√243=34√2
Using the identity cos2R+sin2R=1:
sin2R=(34√2)2=932
Thus,
cos2R=1−sin2R=1−932=32−932=2332
So,
cosR=√2332≈0.8477
For constructive interference in thin films, the condition is given by:
2μtcosR=nλ
For minimum thickness, we take n=1:
t=λ2μcosR
Substituting the known values:
t=5.4×10−72×43×0.8477
Calculating the denominator:
2×43×0.8477≈83×0.8477≈2.259
Thus,
t≈5.4×10−72.259≈2.39×10−7m
The minimum thickness of the soap film is approximately:
t≈2.39×10−7m or 239nm
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (1)23videos
WAVE OPTICAL
- BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (2)10videos
WAVE OPTICAL
- BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION12videos
SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS
Similar Questions
White light is incident on a soap film of μ=4/3 at an angle of 30∘. On examining the transmitted light with a spectrometer a dark band of wavelength 5.5×10−7 m is found. Find the minimum thickness of the film.
View SolutionWhite light is incident on a soap film at an angle of 60∘. On examining the reflecting light by a spectroscope, a dark band corresponding to wavelength 6200Å is found. Find the minimum thickness of the film. Take refractive index of film = 1.33.
View Solution
Knowledge Check
- Question 1 - Select One
A ray of light is incident at an angle of 45∘ (ralative to the normal) on a thin film of a liquid with an index of refraction of √2. Assuming that the medium of both sides of the film is air, find the minimum thickness of the film required for constructive interference in the reflected light for sodium light of wavelenght 600 nm.
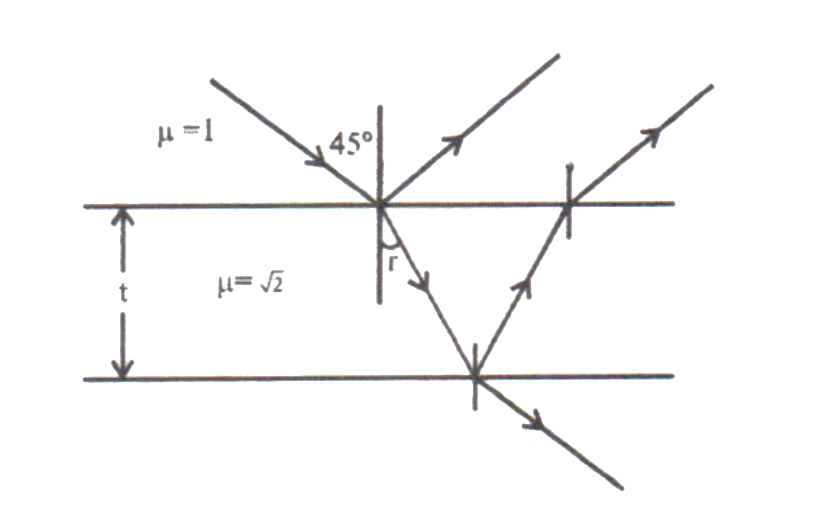 A122 nmB212 nmC173 nmD320 nm
A122 nmB212 nmC173 nmD320 nm
A soap film of μ=43 is illuminated by white light incident at an angle of 45∘. The transmitted light is examined by spectrospe and bright fringe is found to be for wavelength of 6000Å. Find the minimum thickness of the film.
View SolutionA soap bubble of µ=4/3 is illuminated by white light incident at an angle of 30∘. The transmittedlight is examined by a spectroscope and bright band is found for a wavelength of 6000 Å. Find the thickness of the film.
View SolutionA soap film is illuminated by while light incient at an angle of 30∘. The reflected light is examined by a spectroscope in which a dark band corresponding to wavelength 6000Å is found . Calculate the minimum thickness of the film. Given refractive index of film=43
View SolutionWhite light is incident on a soap film at an angle of sin−145 and the reflected light on examination by the spectroscope shows dark bands. The consecutive dark bands corresponds to wavelength 6100 Å and 6000 Å. If the refractive index of the film is 4/3, calculate its thickness.
View SolutionWith a thin air film between two points, 6 fringes appear when light of wavelength 5890 Å is used. Calculate the difference in the thickness of the film between the two points.
View SolutionWhite light incident perpendicular on a soap film gets reflected . It has an interference maximum at 5800Å and a minimum at 4200Å in a visible spectrum. If there is no minimum in between the two bands, find the thickness of the soap film. Take refractive index of film = 4/3.
View SolutionVisible light of variable wavelength is incident normally on a thin sheet of plastic in air. The reflected light has a minima only for lamba=512 nm and λ=640 nm in the visible spectrem. What is the minimum thickness (in mum) of the film (μ=1.28) ?
View Solution

