To reduce the intensity of incident unpolarised light to 1/4, find the angle at which the axes of two polaroids should be placed.
To solve the problem of reducing the intensity of incident unpolarized light to 14 using two polaroids, we can follow these steps:
Step 1: Understand the behavior of unpolarized light through a polarizer
When unpolarized light passes through a single polarizer, the intensity of the transmitted light is reduced to half of the incident intensity. If the initial intensity of the unpolarized light is I, then after passing through the first polarizer, the intensity I1 is given by:
I1=I2
Step 2: Apply Malus's Law for the second polarizer
When the light passes through a second polarizer at an angle θ with respect to the first polarizer, the intensity I2 of the light after the second polarizer can be calculated using Malus's Law:
I2=I1cos2(θ)
Substituting I1 from Step 1:
I2=I2cos2(θ)
Step 3: Set the desired intensity
We want the final intensity I2 to be I4:
I2cos2(θ)=I4
Step 4: Simplify the equation
We can cancel I from both sides (assuming I≠0):
12cos2(θ)=14
Step 5: Solve for cos2(θ)
Multiplying both sides by 2 gives:
cos2(θ)=12
Step 6: Find the angle θ
Taking the square root of both sides, we have:
cos(θ)=1√2
This implies:
θ=45∘
Conclusion
The angle at which the axes of the two polaroids should be placed to reduce the intensity of the incident unpolarized light to 14 is 45∘.
---
When unpolarized light passes through a single polarizer, the intensity of the transmitted light is reduced to half of the incident intensity. If the initial intensity of the unpolarized light is I, then after passing through the first polarizer, the intensity I1 is given by:
I1=I2
When the light passes through a second polarizer at an angle θ with respect to the first polarizer, the intensity I2 of the light after the second polarizer can be calculated using Malus's Law:
I2=I1cos2(θ)
Substituting I1 from Step 1:
I2=I2cos2(θ)
We want the final intensity I2 to be I4:
I2cos2(θ)=I4
We can cancel I from both sides (assuming I≠0):
12cos2(θ)=14
Multiplying both sides by 2 gives:
cos2(θ)=12
Taking the square root of both sides, we have:
cos(θ)=1√2
This implies:
θ=45∘
The angle at which the axes of the two polaroids should be placed to reduce the intensity of the incident unpolarized light to 14 is 45∘.
Topper's Solved these Questions
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (A. MULTIPLE CHOICE QUESTIONS)
Explore 25 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS) -AIPMT/NEET & OTHER STATE BOARDS FOR MEDICAL ENTRANCE
Explore 10 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:Revision Exercises (Long Answer Questions)
Explore 9 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
What is meant by a linearly polarised light? Which type of waves can be polarised? Briefly explain a method for producing polarised light. Two polaroids are placed at 90∘ to each other and the intensity of transmitted light is zero. What will be the intensity of transmitted light when one more polariod is placed between these two bisecting the angle between them ? Take intensity of unpolarised light as l0
View Solution(a) When an unpolarised light of intensity I0 is passed through a polaroid, what is the intensity of the linearly polarised light ? Does it depend on the orientation of the polaroid ? Explain your answer.
(b) A plane polarised beam of light is passed through a polaroid. show graphically the variation of the intensity of the transmitted light with angle of rotation of the polaroid in complete one rotation.
View Solution
Knowledge Check
Find the final intensity of light (I"), if the angle between the axes of two polaroids is 60∘.
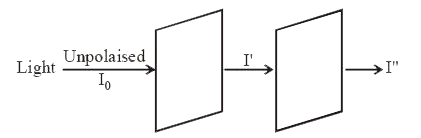 A3I02BI02CI04DI08
A3I02BI02CI04DI08Two polaroids are placed in the path of unpolarised light of intensity I0 such that no light is emitted from the second polaroid. If a third polaroid, whose pass axis makes an angle θ with the pass axis of first polaroid, is placed between these polaroid then the intensity of the light emerging from the last polaroid will be
AI08sin22θBI04sin22θCI02cos4θDI0cos2θThe polariser and analyser are inclined to each other at 60∘. The intensity of polarised light emerging from polariser is I. The intensity of the unpolarised light incident on the polariser is
AI0B34I0C12I0D14I0
Two crossed polarod A and B are placed in the path of a beam of unpolarized light . In between these two polaroid, a third polaroid C is placed such that its principal section is at an angle of 60∘ with that of A. What percentage of intensity of incident unpolarized light emerges from C and B ?
View SolutionAn unpolarized beam of light has intensity I0 . It is incident on to ideal polarizing sheets . The angle between the axes of polarization of these sheets is θ . Find θ if the emerging light has intensity I0/4)
View SolutionUnpolarised light passes through a polariser and analyser which are at an angle of 45∘ with respect to each other. The intensity of polarised light coming fromanalyse is 5W/m2 . The intensity of unpolarised light incident on polariset is
View SolutionWhen an unpolarised light of intensity I0 is incident on a polarising sheet, the intensity of the light which does not get transmitted is
View SolutionThe polariser and analyser are inclined to each other at 60∘. The intensity of polarised light emerging from polariser is I. The intensity of the unpolarised light incident on the polariser is
View Solution