There is a parallel beam of light of larger aperture . Let I be the intensity of light . Perfectly reflecting sphere of radius r is kept in the path of this parallel beam . Find the force exerted by the light beam on sphere .

Video Solution

Text Solution

Verified by Experts

Let us select a reference line OA opposite to the direction of incident beam. Here O is centre of the sphere .

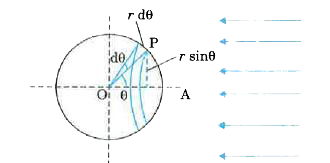
Let us select a radius OP of sphere at an angle $θ$ with the reference line OA . Rotate this radius OP around OA to get a circle on sphere . Now increase this angle to $θ + d t e t h a$ and again rotate OP about OA to get one more circle. Radius of this circular ring segment is $r sin t e t h a$ .
Total are of this ring segment will be $2 π (r sin θ) (rd θ) = 2 π r^{2} sin θ d θ .$
It we select some are $Δ A$ , then corresponding linear momentum falling on the same surface will be $Δ U / c$ . Light will be reflected at the smae angle with the normal and hence change in linear momentum can be written as follows :
$Δ p / Δ t = (2 / c) I Δ A {cos}^{2} θ$
The above expression is basically for the force acting on $Δ A$ portion of ring segment . This force acts perpendicular to the surface of the ring. And from symmetry , we can understand that components perpendicular to OA will be canalled and these along OA will be added, hence contribution of this force to the total force will be just component perpendicular to beam and can be written as follows :
$(Δ p / Δ t) cos θ = (2 / c) I Δ A {cos}^{3} θ$
Now we can replace $Δ A$ with the total area of ring segment to get the force exerted on selected ring segment.
$d F = (2 / c) I (2 π r^{2} sin θ d θ) {cos}^{3} θ$
We can calculate total force on sphere by integrating the above relation for $θ = 0^{\circ} to 90^{\circ}$ because light is falling on the front portion of the sphere.
$F = \frac{4 π r^{2} I}{c} \int_{0}^{π / 2} {cos}^{2} θ (sin θ d θ)$
$F = \frac{4 π r^{2} I}{c} \int_{0}^{π / 2} {cos}^{2} θ (sin θ d θ) ... (i)$
Let $t = cos θ \Rightarrow d t = - sin θ d θ$
Substituting above values in equation (i) , we get the following :
$F = \frac{4 π r^{2} I}{c} {[\frac{t^{3}}{4}]}_{1}^{0}$
$\Rightarrow F = \frac{π r^{2} I}{c}$

Updated on:21/07/2023

A perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
A $\frac{2 π R^{2} l}{c}$
B $\frac{π R^{2} l}{c}$
C $\frac{4 π R^{2} l}{c}$
DNone of these
A parallel beam of light falling on the eye gets focused on the retina because of refractions at
Athe cornea
Bthe crystalline lens
Cthe vitreous humor
Dvarious surfaces in the eye
A parallel beam of light falls on a solid tranparent sphere.

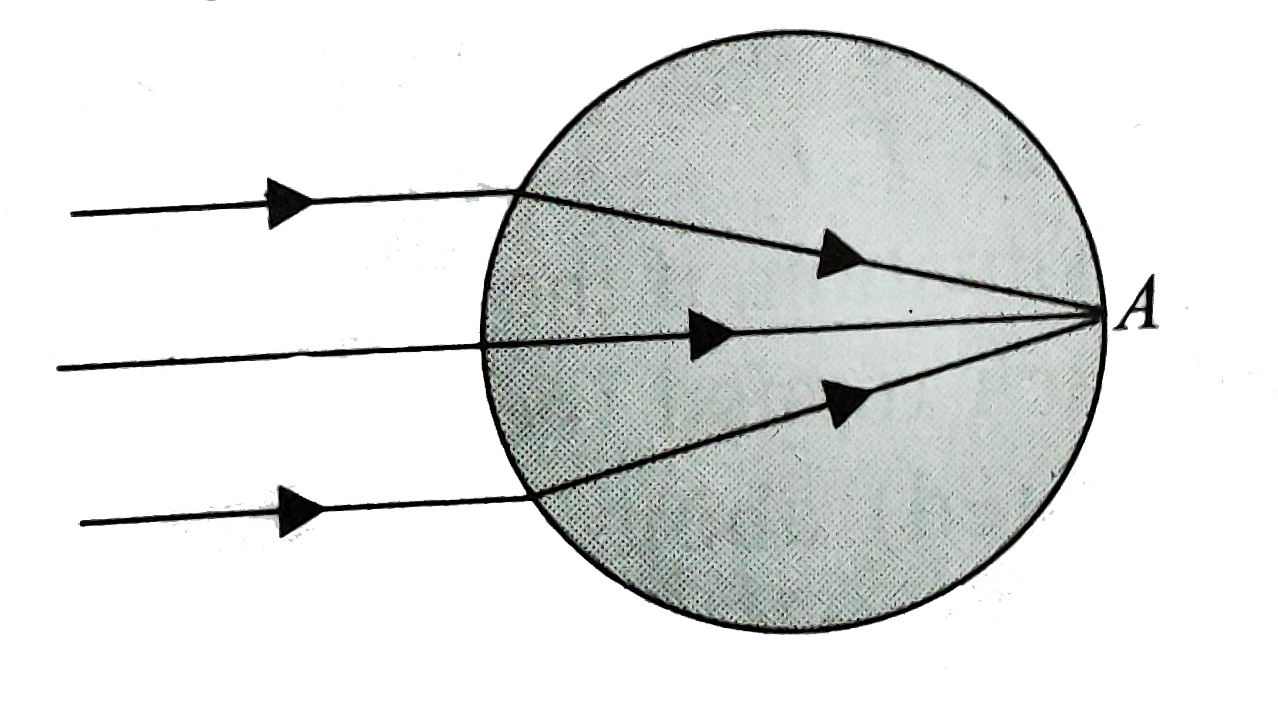
Q. Which is corret?
AIf the beam is thick, then whole beam can be focussed at A.
Bthe whole beam can be focussed at A only if the beam is thin enough
Cif the beam is thin, then the beam can't be focussed before A.
Dnone of these