Derive de Broglie wave equation for material particles.
(b) Why does photoelectric emission not take place if the frequency of incident radiation is less than threshold frequency ?
Step-by-Step Solution
1. Understanding the Concept:
- According to de Broglie's hypothesis, every moving particle or object has an associated wave. The wavelength (λ) of this wave is inversely proportional to its momentum (p).
2. Using Einstein's Mass-Energy Relation:
- The mass-energy equivalence is given by the equation:
E=mc2
- This equation relates the energy of a particle to its mass (m) and the speed of light (c).
3. Using Planck's Relation:
- The energy of a photon can also be expressed as:
E=hν
- Here, h is Planck's constant and ν is the frequency of the radiation.
4. Relating Frequency and Wavelength:
- The frequency can be related to the wavelength (λ) and the speed of light (c) by:
ν=cλ
5. Equating the Two Energy Expressions:
- Setting the two expressions for energy equal gives:
mc2=hν
- Substituting ν=cλ into this equation:
mc2=h(cλ)
6. Rearranging the Equation:
- Rearranging the equation to solve for λ:
mc2λ=hc
- Dividing both sides by mc:
λ=hmv
- Here, v is the velocity of the particle.
7. Final Expression:
- Thus, the de Broglie wavelength (λ) for a material particle is given by:
λ=hmv
Part (b): Explanation of Photoelectric Emission and Threshold Frequency
1. Understanding Photoelectric Emission:
- Photoelectric emission refers to the phenomenon where electrons are emitted from a material (usually a metal) when it is exposed to light of sufficient frequency.
2. Threshold Frequency:
- The threshold frequency (ν0) is the minimum frequency of incident light required to eject electrons from the surface of the material.
3. Work Function:
- The work done (W) to remove an electron from the surface is given by:
W=hν−hν0
- Here, W is the kinetic energy of the emitted photoelectron.
4. Condition for Emission:
- For photoelectric emission to occur, the energy of the incident photon (given by hν) must be greater than the work function (given by hν0):
hν>hν0
5. When Frequency is Less than Threshold Frequency:
- If the frequency of the incident radiation is less than the threshold frequency (ν<ν0), then:
W=hν−hν0<0
- This implies that the kinetic energy of the emitted electron would be negative, which is not physically possible.
6. Conclusion:
- Therefore, no photoelectric emission occurs if the frequency of the incident radiation is less than the threshold frequency, regardless of the intensity of the radiation.
- According to de Broglie's hypothesis, every moving particle or object has an associated wave. The wavelength (λ) of this wave is inversely proportional to its momentum (p).
- The mass-energy equivalence is given by the equation:
E=mc2
- This equation relates the energy of a particle to its mass (m) and the speed of light (c).
- The energy of a photon can also be expressed as:
E=hν
- Here, h is Planck's constant and ν is the frequency of the radiation.
- The frequency can be related to the wavelength (λ) and the speed of light (c) by:
ν=cλ
- Setting the two expressions for energy equal gives:
mc2=hν
- Substituting ν=cλ into this equation:
mc2=h(cλ)
- Rearranging the equation to solve for λ:
mc2λ=hc
- Dividing both sides by mc:
λ=hmv
- Here, v is the velocity of the particle.
- Thus, the de Broglie wavelength (λ) for a material particle is given by:
λ=hmv
- Photoelectric emission refers to the phenomenon where electrons are emitted from a material (usually a metal) when it is exposed to light of sufficient frequency.
- The threshold frequency (ν0) is the minimum frequency of incident light required to eject electrons from the surface of the material.
- The work done (W) to remove an electron from the surface is given by:
W=hν−hν0
- Here, W is the kinetic energy of the emitted photoelectron.
- For photoelectric emission to occur, the energy of the incident photon (given by hν) must be greater than the work function (given by hν0):
hν>hν0
- If the frequency of the incident radiation is less than the threshold frequency (ν<ν0), then:
W=hν−hν0<0
- This implies that the kinetic energy of the emitted electron would be negative, which is not physically possible.
- Therefore, no photoelectric emission occurs if the frequency of the incident radiation is less than the threshold frequency, regardless of the intensity of the radiation.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Revision Exercises (Long Answer Questions)
3 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Revision Exercises (Numerical Problems)
20 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Revision Exercises (Fill in the Blanks)
11 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
Similar Questions
The de Broglie wavelenght (λ) associated with a photoelectron varies with the frequency (v) of the incident radiation as,[v0 is threshold frequency]:
View SolutionPhotoelectric work function for a surface is 2.4 eV. Light of wavelength 6.8×10−7m shines on the surface. Find the frequency of incident light and also the threshold frequency. Will there be photoelectric emission or not ?
View Solution
Knowledge Check
Assertion : The threshold frequency of photoelectric effect supports the particle nature of light.
Reason : If frequency of incident light is less than the threshold frequency, electrons are not emitted from metal surface.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.Assertion : The threshold frequency of photoelectric effect supports the particle nature of sunlight .
Reason : If frequency of incident light is less than the threshold frequency , electrons are not emitted from metal surface.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion and reason both are false.According to Einstein's photoelectric equation, the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is
A B
B C
C D
D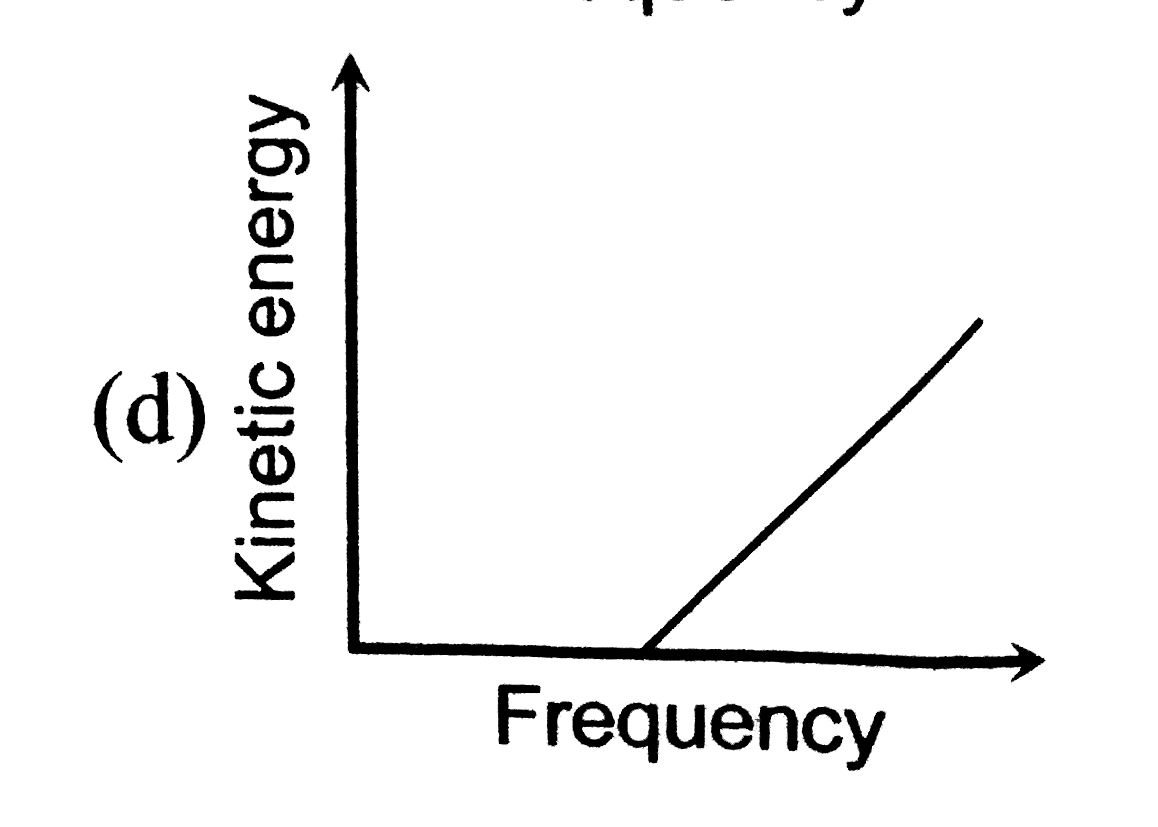
Explain how Einstein's photoelectric equation enables us to understand the (i) linear dependence, of the maximum K.E. of the emitted electrons, on the frequency of the incident radiations (ii) existance of a threshold frequency for a given photoemitter.
View SolutionAccording to Einstein's photoelectric equation, the graph between kinetic energy of photoelectrons ejected and the frequency of the incident radiation is :
View SolutionState how in a photo-cell, the work function of the metal influence the kinetic energy of the emitted electrons.
(a) If the intensity of the incident radiation is doubled, what change occur in (i) the stopping potential and (ii) in photoelectric current?
(b) If the frequency of the incident radiation is doubled, what changes occur in the (i) stopping potential and (ii) photoelectric current.
View SolutionDoes the 'stopping potential' in photoelectric emission depend upon
(i) the intensity of the incident radiation in a photocell. ?
(ii) The frequency of the incident radiation ?
View SolutionAssertion: Kinetic energy of photoelectrons emitted by a photosensitive surface depends upon the frequency of incident photons, provided that it is greater than the threshold frequency.
Reason: Number of photoelectrons depends on the intensity of incident radiation.
View Solution
