A particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance of the particle from the origin as F(x)=−kx+ax3. Hence k and a are positive constants. For 20. the functional form of the potential energy U(x) of the particle is:




The correct Answer is:d
Here, F(x)=kx+ax3
Also, we know that F(x)=−dUdx
∴P.E.,U=−∫F.dx
=−∫(−kx+ax3)dx
U=kx22−ax44
This follows that U=0 at two valves of x i.e.
kx22−ax44=0
x22[k−ax22]=0
∴ x=0 and x=√2ka.
This means the graphs (b) and (c) are not possible.
Further U is maximum or minimum, when dUdx=0.
i.e. −(−kx+ax3)=0
kx−ax3=0
x(k−ax2)=0
∴ either x=0 or x=√ka.
For the value of √ka=x, U will be max.,
Where d2Udx2<0
Now d2Udx2=ddx(kx−ax3)=k−3ax2
=k−3a(√ka)2=−2k
Thus, U is max. at x=√ka and minimum negative for x>√2ka.Hence graph (a) is also ruled out.
Topper's Solved these Questions
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Multiple Choice Questions (LEVEL-III)
5 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Recent Competitive Questions
8 Videos
- WORK , POWER , ENERGY AND COLLISIONSBOOK - MODERN PUBLICATIONCHAPTER - WORK , POWER , ENERGY AND COLLISIONSEXERCISE - Revision Test
40 Videos
- WAVE OPTICS BOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICS EXERCISE - Recent Competitive Questions
18 Videos
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)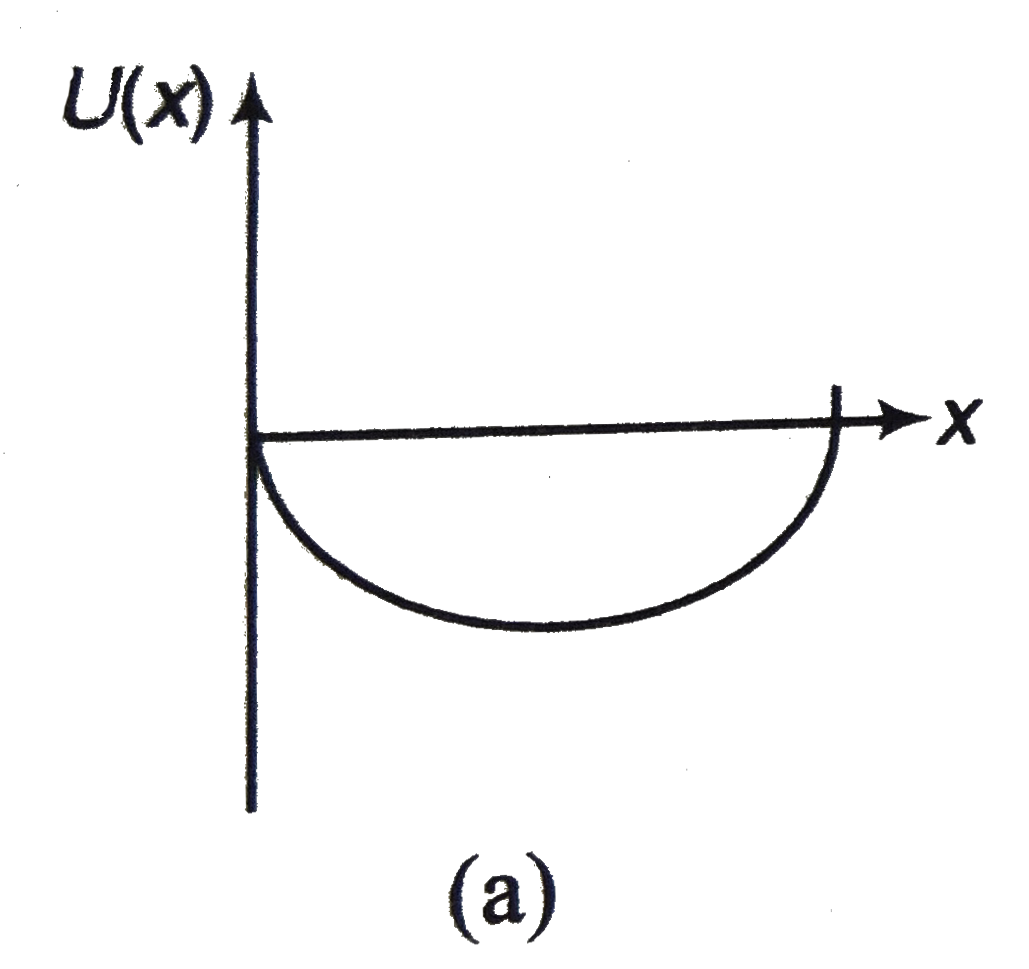 , (b)
, (b) 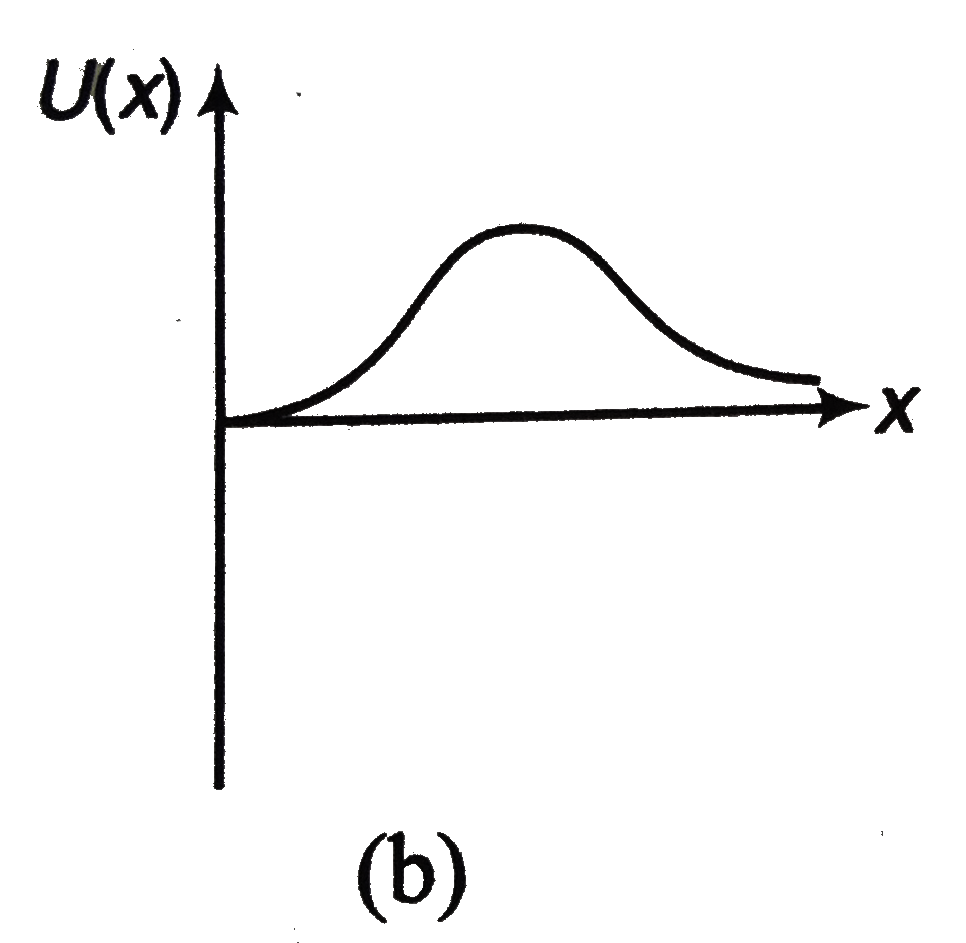 , (c)
, (c) 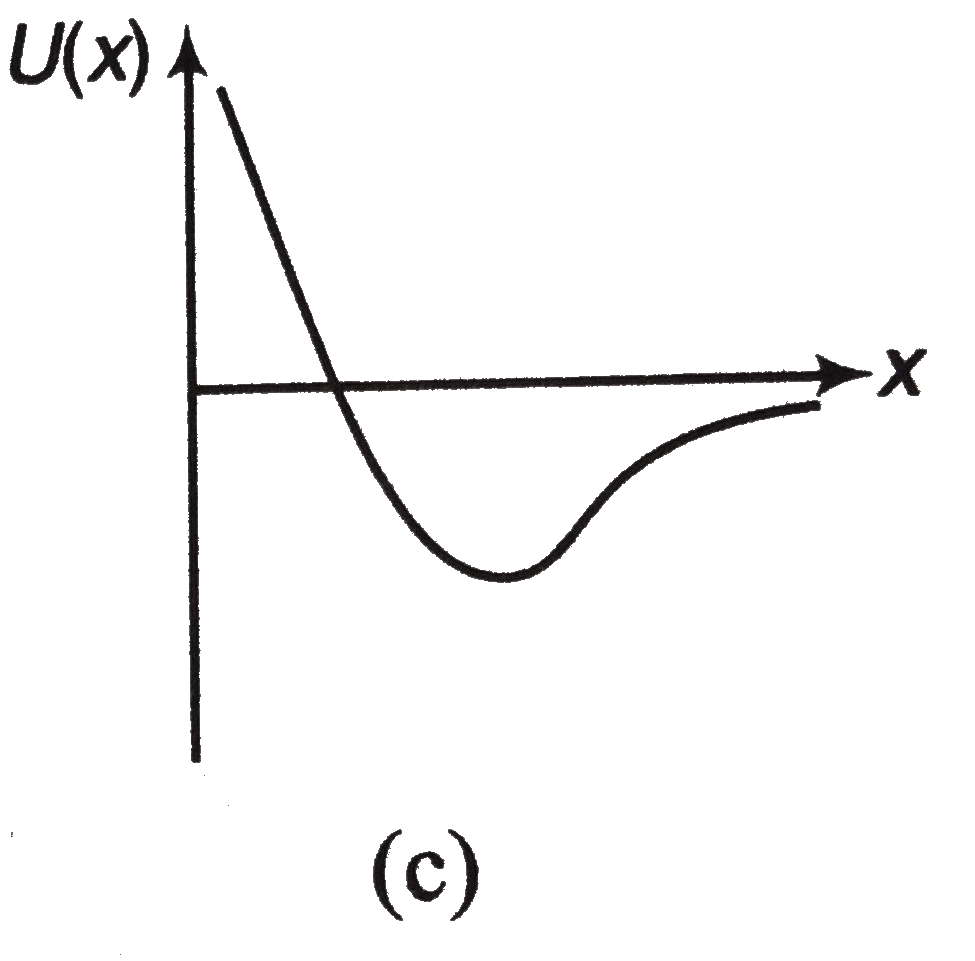 , (d)
, (d) 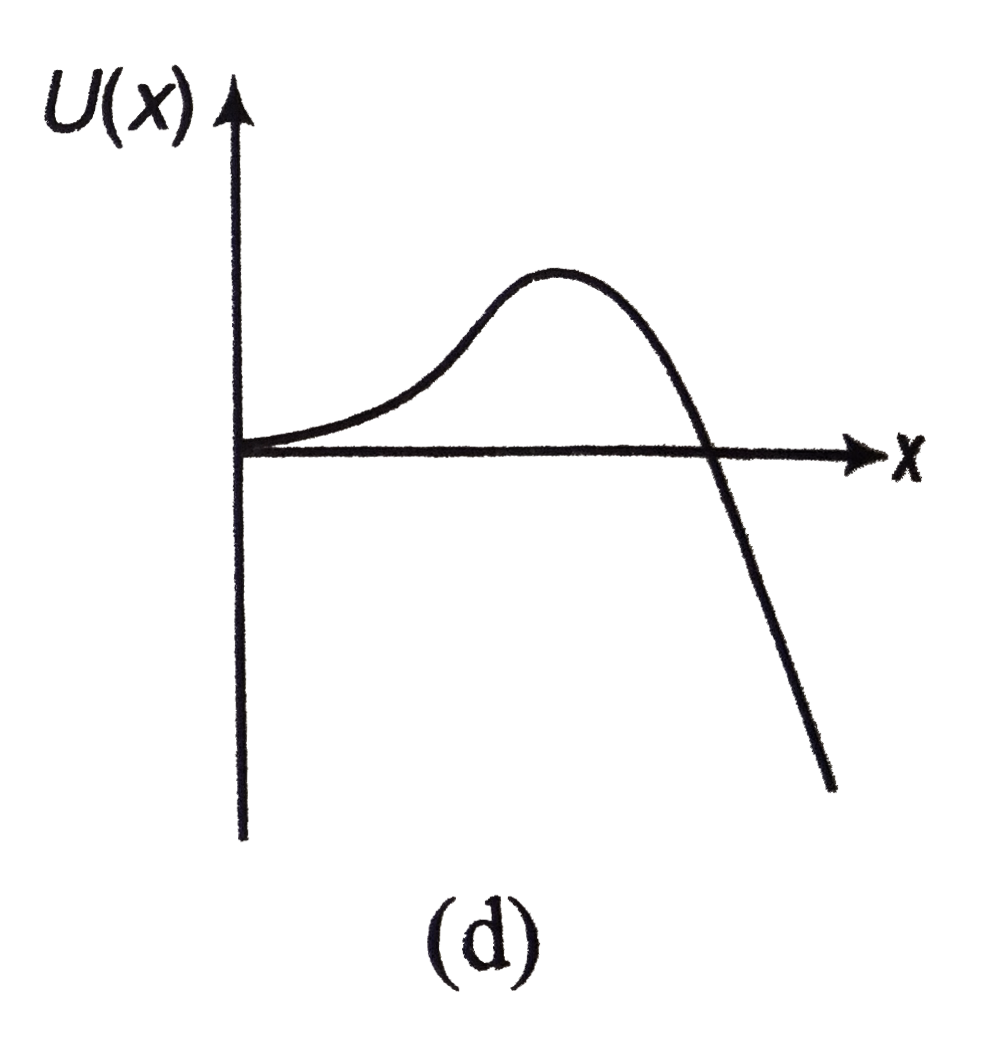 .
.
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a) , (b)
, (b)  , (c)
, (c)  , (d)
, (d)  .
.
View Solution
Knowledge Check
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B C
C D
D
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B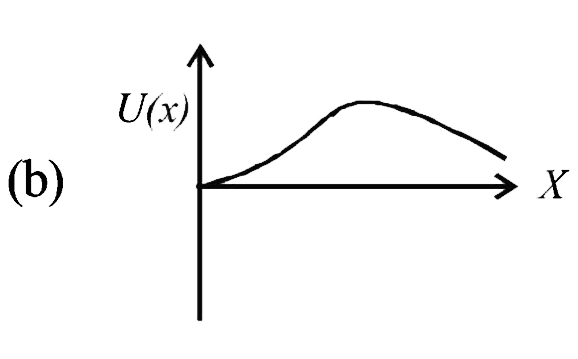 C
C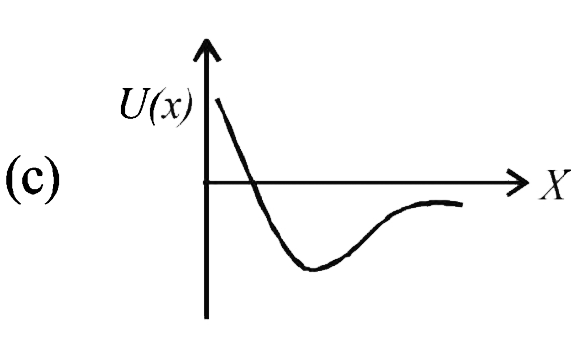 D
D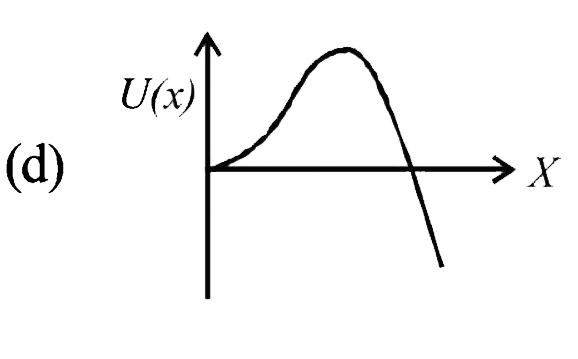
A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A B
B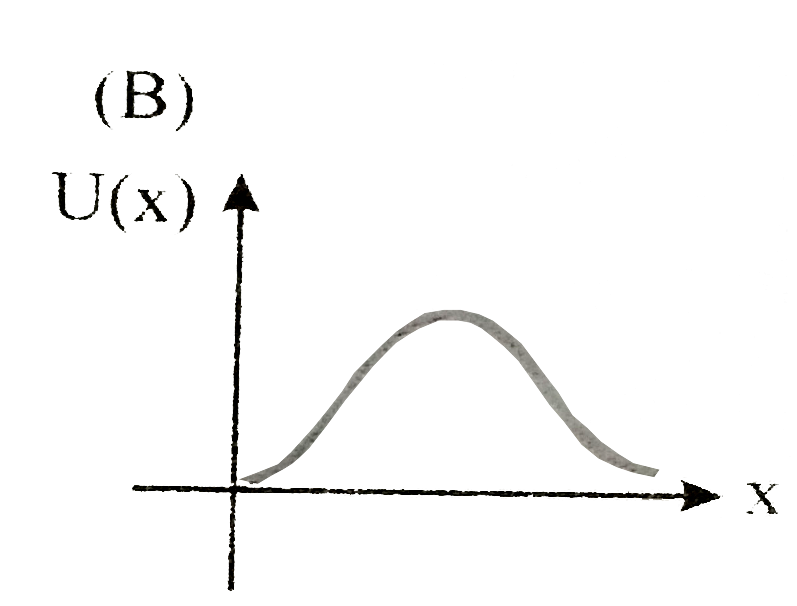 C
C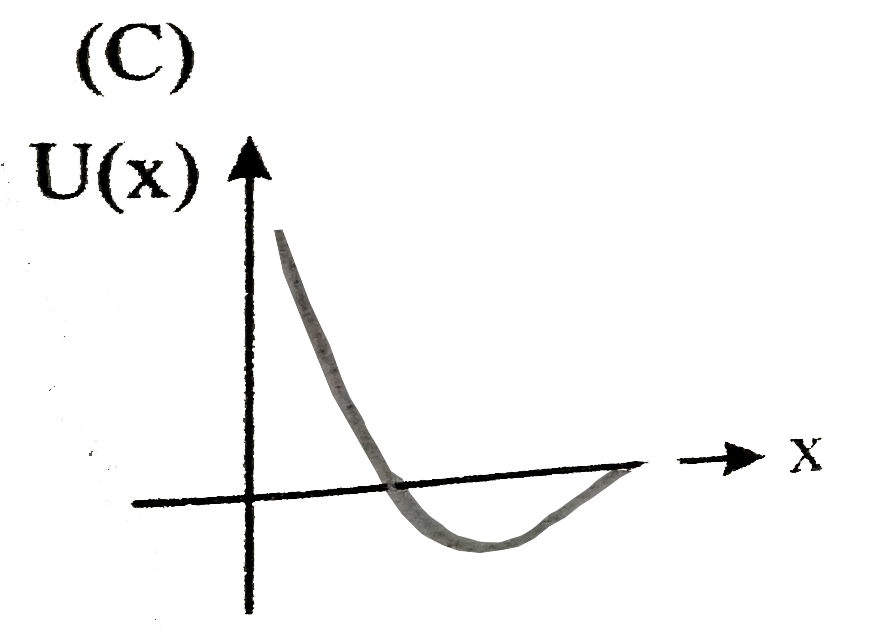 D
D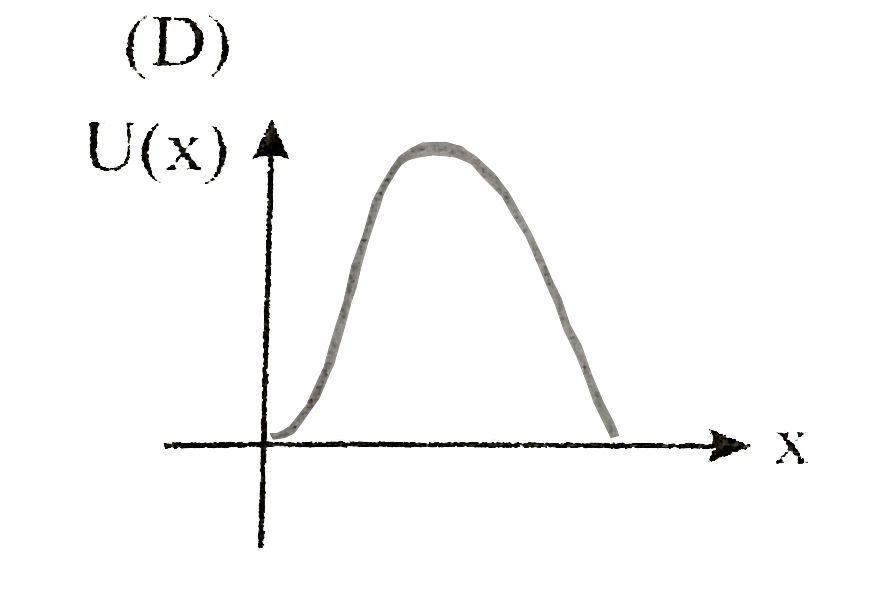
A particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View Solution
