A cylinder of mass M and radius R starts falling freely under gravity at t=0 as shown in fig. The tension in each string at any given times is T. What is value of 'T' ?

Mg
Mg2
Mg4
Mg6
The correct Answer is:D
Let M be the mass of the cylinder falling under gravity.
The equation of motion will be
Mg−2T=Ma ...(i)
If we consider the torque by each force of tension then
2T:R=1α=12MR2.aR
or a=4TM
Putting in (i)
Mg=Ma+2T
=M×4TM+2T
=6T
∴T=Mg/6
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
A cylinder of mass 0.6kg and radius R is falling under gravity without slipping as the thread is unfolding.Find the tension in the thread (in newton).
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View Solution
Knowledge Check
A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A2Mg/3BMg/2CMg/3DMg/6A string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
AMg6BMg3CMg2D2Mg3A particle is falling freely under gravity. In first t second it covers distance x1 and in the next t second, it covers distance x2, then t is given by
A√x2−x1gB√x2+x1gCsqrt((2(x_2-x_1))/g)D√2(x2+x1)g
A cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA uniform cylinder of mass m and radius R starts descending at a moment t=0 due to gravity, Neglecting the mass of the thread, find
(a) the tension of each thread and the angular acceleration of the cylinder,
(b) the time dependence of the instantaneous power developed by the gravitational force.

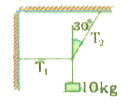
View SolutionA block of mass 10 kg is suspended with two strings as shown in the fig. Find the tensions T1andT2 in the two string.
View SolutionA string is wrapped around a cylinder of mass M and radius R. The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
View SolutionA particle is falling freely under gravity. In first t second it covers distance x1 and in the next t second, it covers distance x2, then t is given by
View Solution
